Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
The two main properties of a cube are:
A cube has 12 edges, 6 faces, and 8 vertices.
All the faces of a cube are square-shaped.
What is the formula for the area of the base of a cube?
If the side of a cube is a, the formula for the area of the base will be a².
What is the formula for the volume of a cube using the diagonal?
If the length of the diagonal of a cube is d, the formula for the volume of the cube will be = (√3×d³)/9.
Cube: Definition, Properties, Formulas, and Solved Examples
Cube is a 3D geometric shape with six equal square faces. Understand the cube properties, formulas, and real-life applications to improve your skills.
Chandni 9 Jun, 2025
Share
What is Cube: A cube is a three-dimensional geometric shape enclosed by six plain surfaces, and each of these surfaces is a perfect square. The length, width, and height of a cube are equal.
In real life, we often encounter a cube such as ice cubes, dice, Rubik's cube, etc. The cube holds significant importance in both mathematics and geometry due to its simplicity and symmetry.
A cube is a solid geometrical shape that has six faces, 12 sides, and eight vertices. It is also called an equilateral cuboid because all 12 sides are of equal length. In a cube, the angle between adjacent surfaces is 90 degrees. The edges are the common boundaries where two surfaces meet, and vertices are the points where two sides meet.
The characteristics of cube can be summarized as below:
Faces: It has six square faces. Each face meets the other four faces.
Edges: There are twelve edges, all of equal length.
Vertices: It has eight vertices where three edges meet at right angles.
Angles: The internal angle between adjacent faces is a right angle (90°).
The mathematical properties of cube make it a useful subject in geometry. The cube is a 3D shape, the important parameters used to measure the cube are surface area, volume, and diagonals. Let us discuss the cube definition and formula for each of these in detail.
Lateral Surface Area
The lateral surface area of a cube is the total area of all 4 square side faces. It is measured in square units. The total surface area of the cube can be calculated as follows:
Let the edge (side) of the cube = a
Area of one face = Area of a square = a x a = a²
The cube has 4 side faces, so the lateral surface area of the cube = 4 a²
Total Surface Area
The total surface area of cube is the total area of all six square side faces. It is measured in square units. It is the area occupied by the cube in the 3D plane. The total surface area of the cube can be calculated as follows:
Let the edge (side) of the cube = a
Area of one face = Area of a square = a x a = a²
The cube has 6 side faces, so the lateral surface area of the cube = 6a²
Volume
The volume of a cube is the amount of space enclosed within it. It is measured by cube units. The volume of a cube can be calculated by finding the cube of the side length of the cube. The formula of the volume of a cube is given by:
The volume of a cube = a³
Where a is the length of each side of the cube
Diagonal
A cube has two types of diagonals: F ace diagonal and M ain diagonal.
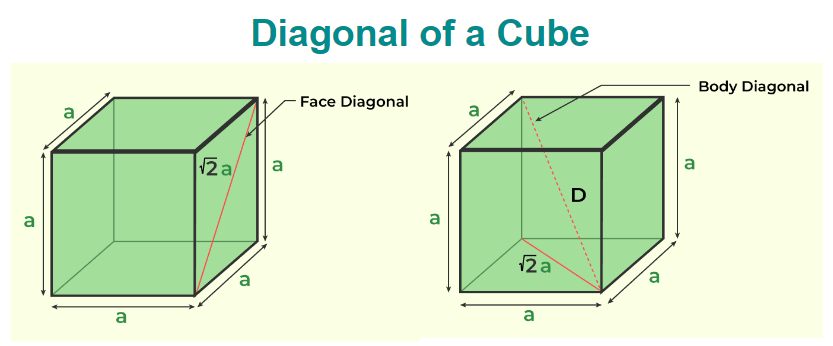
Face Diagonal : On each face, there are two diagonals joining the opposite vertices. Therefore, we have twelve face diagonals for six faces.
Main Diagonal : Four main diagonals connect the opposite vertices of the cube.
Length of face diagonal of the Cube = √2a
Length of the Main diagonal of Cube = √3a
Where 'a' is the side of the cube.
Euler’s Formula
Euler’s Formula expresses the relation between faces, edges, and vertices of a polyhedron. Euler’s formula is given as:
F + V = E + 2
Where F is the number of faces, V is the number of vertices, and E is the number of edges.
For a cube, F= 6, V= 8, E=12
So, the LHS of the expression will be, F + V = 8 + 6 = 14
RHS of the expression will be, E + 2 = 12 + 2 =14
So, Euler’s formula also holds for a cube.
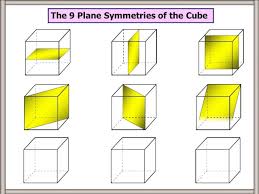
Symmetry of a Cube
A cube has 9 planes of symmetry, each dividing the cube into two identical shapes. These planes of symmetry include symmetry across its faces as well as across the diagonals. Cubes show both rotational and reflective symmetry, making them one of the most widely studied objects in solid geometry.
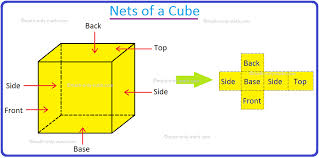
Nets of a Cube
A net is a two-dimensional pattern that can be folded to form a three-dimensional object. For making a cube, there can be 11 different nets, and each net consists of six connected squares that form the six surfaces of the cube. Nets of cubes provide a useful guideline for understanding the relationship between the two-dimensional and three-dimensional geometry of cubes.
Difference B etween a Cube and a Cuboid
Cube and cuboid are solid shapes of a similar nature, but there are a few differences as mentioned below.
Difference B etween a Cube and a Cuboid
Property
Cube
Cuboid
Shape
All faces are squares in a cube
A rectangular shape with six rectangular faces.
Lengths
All lengths (a) are equal
Length (L), Breadth (B), and Height (H) are not same
Volume
a 3
L x B x H
Surface Area
6a 2
2(LB + BH + LH)
Diagonals
√3a
√ (L 2 + B 2 + H 2 )
Cube Solved Examples
1. If the value of the side of the cube is 5 cm, then find its total surface area and volume.
Solution:
Given, side, a = 5 cm
Therefore, using the formula of total surface areas and volume, we can write:
Surface Area = 6a² = 6 × 25 = 150 cm²
Volume = a³ = 5 3 = 125 cm³
2. Find the volume of a Rubik's cube of length 10 cm.
Solution:
The length of the side of the cube = 10 cm
Using the cube formula,
Volume = 10 × 10 × 10 = 10 ³ = 1000 cm³
Cubes Real-World Applications
Cubes have applications in everyday life, especially in the fields of architecture, packaging, engineering, and art, as explained below.
Architecture and Construction : Cubes are frequently used in constructing buildings, monuments, and sculptures. Their uniformity and easy calculation and designing process make them ideal for structural units. They can be combined easily, as seen in modular construction.
Storage and Packaging : Cubes offer optimal space utilization for packing and storage. Whether in shipping containers or product packaging, the uniform dimensions help in arranging items efficiently without wasting space.
Games and Dice : In games of chance like dice games, the cube's six identical faces allow for equal probability in rolls, making it an important element in studying probability and statistics.
Cubes have a typical 3D shape with six square surfaces. It has significant applications in mathematics, physics, architecture, and engineering. They serve as the basis for understanding higher-dimensional structures and play a crucial role in the study of volumetric calculations and symmetry. Join Online Tuition Classes for Kids Now!!
