Mental Maths: Overview, Techniques, Benefits, Tips to Improve
Mental Maths involves performing calculations in your head, improving speed, problem-solving, memory, and confidence in numerical tasks. Check this article to know everything about mental math.
Neha Tanna1 Oct, 2024
Share
Mental Maths: Mental maths is the process of doing mathematical operations alone using the human brain, devoid of the need for calculators or other aids. When calculators are unavailable or the computation time is significantly less than the computation time, people resort to mental maths.
Mental maths can be used to do arithmetic operations quickly for calculations. Primary school students in grades 1 through 5 can practise mental maths by employing shortcuts and time-saving techniques. Specific strategies created for different types of math problems are included in mental math techniques. Since their capacity for mental computation is the greatest, very few people are called mental calculators. The majority of the methods depend on the decimal system of numbers. Which methods to utilise is determined by the choice of radix.What is Mental Maths?
As the name suggests, mental math refers to a combination of skills that allows people to complete arithmetical calculations “in their head” without the assistance of calculators or other resources. Mental maths is helpful in daily life to provide answers to a variety of questions, such as:- What is a certain item's final selling price?
- What is the appropriate quantity of change I should get from the cashier?
- When should I leave so that I may go to a certain location on time?
Related Links -
Mental Maths Techniques
Mental math techniques help in performing calculations quickly in your head without the need for paper or a calculator. Here are some common and useful mental math strategies:Estimation
When performing mental calculations, one must think in terms of scaling. For example, the estimating approach provides the expected number of digits for the final response when the product of the integers 1 531 and 19 625 is obtained. Here's one method to go about doing this. 1 531 is rounded to the nearest thousands = 1500 and 19 625 rounded to the nearest thousands = 20000 So, the result of 1500 × 20000 = 30 000 000 The actual result is 1531 × 19 625 = 30 045 875.Factors
Factors are numbers that divide evenly into another number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Every number has at least two factors: 1 and itself. Prime numbers have only two factors, while composite numbers have more. Factoring is crucial in simplifying fractions, solving equations, and analyzing number properties. For instance, 14 × 15 = 201 is not reasonable. 15 is a multiple of the number 5, 14 is a multiple of the number 2. Hence the product must be an even number. A number that is a multiple of 5 and 2 is a multiple of the number 10. The right answer is 210.Finding differences
i) Direct computation
Consider two numbers a and b. The calculation is performed digit by digit when the second number's digits are smaller than the first number's digits. For example, find the difference of 872 – 41. Subtract 1 from 2 in the one’s place and 4 from 7 in the 10’s place. The final answer is 831.ii) Indirect computation
Indirect computation refers to solving problems by using alternate methods or intermediary steps rather than direct calculation. It often involves breaking a complex problem into simpler parts or using properties of numbers to find the solution. For example, instead of multiplying two large numbers directly, you can decompose one number into smaller components or use approximation methods to get a quicker answer.iii) Borrow method
The borrow method, commonly used in subtraction, helps when the top digit in a column is smaller than the bottom digit. To perform this, you "borrow" 1 from the next higher place value (e.g., the tens column), adding 10 to the smaller digit to allow subtraction. This is typically used in multi-digit subtraction to avoid negative results in individual columns. Subtract the numbers from left to right. For example: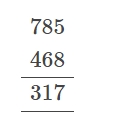
iv] Using square numbers
Using square numbers is a mental math technique that leverages the fact that squaring a number (multiplying it by itself) provides useful reference points for quick calculations. For example:
| 1 2 | 1 | 11 2 | 121 | 21 2 | 441 |
| 2 2 | 4 | 12 2 | 144 | 22 2 | 484 |
| 3 2 | 9 | 13 2 | 169 | 23 2 | 529 |
| 4 2 | 16 | 14 2 | 196 | 24 2 | 576 |
| 5 2 | 25 | 15 2 | 225 | 25 2 | 625 |
| 6 2 | 36 | 16 2 | 256 | 26 2 | 676 |
| 7 2 | 49 | 17 2 | 289 | 27 2 | 729 |
| 8 2 | 64 | 18 2 | 324 | 28 2 | 784 |
| 9 2 | 81 | 19 2 | 361 | 29 2 | 841 |
| 10 2 | 100 | 20 2 | 400 | 30 2 | 900 |
v) Finding roots
Finding roots, particularly square roots or cube roots, involves determining which number, when multiplied by itself (or cubed), gives the original number.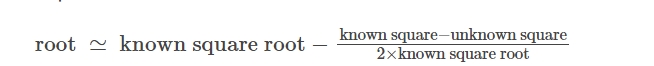
vi) Approximation of common logarithms
Approximating common logarithms (logarithms with base 10) involves estimating the value of a logarithm for numbers that are not exact powers of 10.
Mental Maths FAQs
What are mental math questions?
Mental math is a group of skills that allow people to do math “in their head” without using pencil and paper or a calculator. One of these skills is remembering math facts, like 8 × 5 = 40. Other skills include rounding numbers and estimating calculations.
What is another name for mental math?
Mental math is the ability to perform mathematical calculations in your mind. It is also known as mental arithmetic, mental calculation, quick math, fast math, or doing math in your head. In German, it is known as Kopfrechnen, which translates into English as “head calculation”.
What is the fastest mental math system?
Vedic mathematics
Does mental math improve memory?
Mental arithmetic is a great tool for training the memory and concentration.
Why do we need mental math?
Mental arithmetic enables children to visualize numbers and make calculations mentally.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.