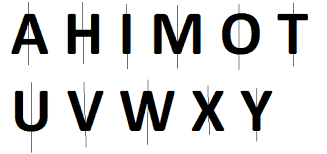Vertical Line in Coordinate Geometry: Definition, Equation, and Examples
A vertical line is a standing line that runs from top to bottom or from bottom to top and is parallel to the y-axis in a coordinate plane. Explore more about vertical lines here.
Chandni 20 Jun, 2025
Share
A Vertical line is a straight line that runs from top to bottom or from bottom to top and is perpendicular to a surface, or another line considered the base.
For example, the y-axis in a graph is a vertical line because it stands upright and forms a right angle with the x-axis, which acts as the base. Vertical lines are often called standing lines due to their straight, upright position.Vertical Lines in Real Life
Vertical lines are all around us in our everyday lives. You can see them in tall buildings, tree trunks, and table or chair legs. These are common vertical line examples in the real world.
Properties of Vertical Lines
Vertical lines have several distinct properties:- Vertical lines run up and down, always staying parallel to the y-axis. They do not cross or intersect the y-axis at any point.
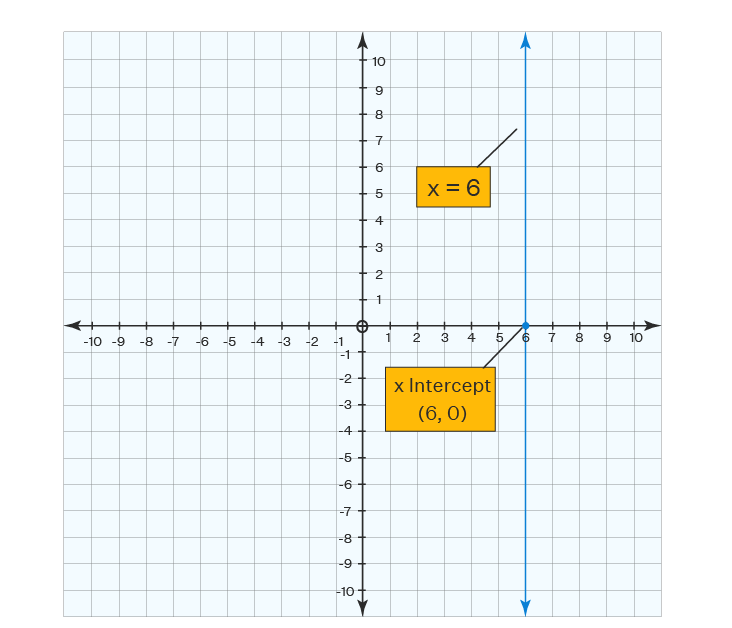
- The equation of a vertical line is written as x = a, where a is a fixed real number. This means the x-coordinate for every point on the line is the same, and the y-coordinate can vary.
- The slope of a vertical line is undefined because the line does not move horizontally (there is no change in the x-coordinate). The run (horizontal change) is zero, so dividing by zero results in an undefined slope.
- When a vertical line intersects a horizontal line, they meet at a 90-degree angle, forming a right angle.
How to Draw Vertical Line?
Thinking about how to draw vertical line accurately? Drawing a vertical line is simple and can be done using either a ruler or a coordinate grid. Here’s how:Drawing a Vertical Line Using a Ruler
Step 1: Place the ruler in a standing position perpendicular to the edge of the page. Step 2: Draw the line by moving your pencil from bottom to top or top to bottom along the ruler's edge.Drawing a Vertical Line On a Coordinate Plane
To draw a vertical line on a coordinate grid, follow these steps: Plot a Point : Start by marking any point on the grid. For instance, plot the point (5,3). Identify the x coordinate: Note the x-coordinate of the plotted point (in this case, 5). Plot Another Point : Plot a second point with the same x coordinate but a different y coordinate, such as (5,−2). Join the Points : Use a ruler to connect the two points. The resulting line will be vertical, parallel to the y-axis.Uses of Vertical Lines
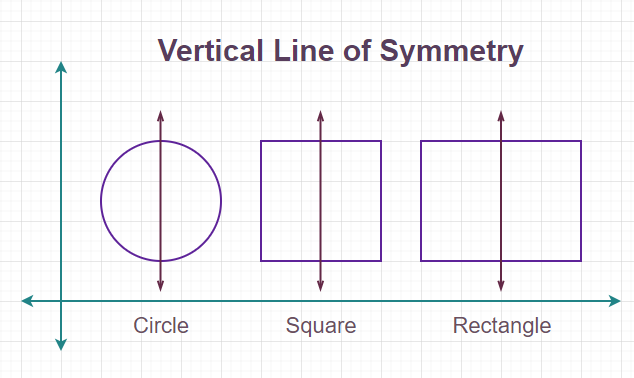
Vertical lines are widely used in various areas, from art and design to photography. They help create symmetry, emphasize height, and structure images in meaningful ways. Here are two common uses of vertical lines:Uses of Vertical Line in Symmetry
Vertical line symmetry occurs when a shape can be divided into two identical halves by a straight line running down the middle. This line is called the mirror line because placing a mirror on it would show the hidden half of the shape.
Examples of shapes with vertical line symmetry include circles, squares, and rectangles
Some English letters with vertical line symmetry are A, H, I, M, O, T, U, V, W, X, Y
Slope of Vertical Lines
In coordinate geometry, the slope of a line is calculated by dividing the change in the y-coordinate (rise) by the change in the x-coordinate (run). The x-coordinate stays the same for all points for vertical lines, meaning the change in x (run) is always 0. For example, if you consider a vertical line passing through x = 4, the x-coordinate remains 4 no matter the y value. As you move along the line, the y coordinate changes, but there is no change in the x coordinate. This results in a zero run, making the slope undefined. In other words, since there's no horizontal movement, the slope can't be calculated, that’s why we say the slope of a vertical line is undefined.
Difference Between Horizontal and Vertical Lines
The table below shows the comparison between horizontal and vertical lines:| Difference Between Horizontal and Vertical Lines | ||
| Aspects | Vertical Line | Horizontal Line |
| Alignment | Runs parallel to the Y-axis | Runs parallel to the X-axis |
| Slope | Undefined | Always zero |
| Standard Form | Represented by x=a constant | Represented by y=a constant |
| Direction | Moves from top to bottom, or bottom to top | Moves from left to right, or right to left |
| Axis Intersection | Meets the X-axis at one specific point | Meets the Y-axis at one specific point |
| Appearance on Graph | Straight line oriented vertically | Straight line oriented horizontally |
| Examples | Equations include x=−2x or x = 7 | Equations include y= 3 or y=−6 |
| Angle with X-axis | Forms a 90° angle | Forms a 0° angle |
| Angle with Y-axis | Forms a 0° angle | Forms a 90° angle |
Join Online Kids Tuition Class Now !!
| Related Articles | |
| Subtraction Sums | Word Problems |
| What is an Abacus? | Math Puzzles |
| Multiplication Worksheets : | Multiplication Sums |
Vertical Line FAQs
What happens if a vertical line intersects another line?
When a vertical line intersects any other line (except parallel vertical lines), it creates a point of intersection. The point indicates the specific x-coordinate where the lines meet, and this helps in determining solutions in systems of equations.
Do vertical lines ever intersect the y-axis?
Vertical lines do not intersect the y-axis unless the line passes through the origin, where both x and y are zero.
Can a vertical line be angled?
No, vertical lines are strictly straight up and down. They have no angle.
What happens when a vertical line crosses another line?
When a vertical line crosses another line, it creates a point where the two lines meet, showing the x-coordinate of the intersection.
What are some examples of vertical lines in nature?
Examples of vertical lines in nature include tree trunks, waterfalls, mountain peaks, cactus plants, and steep cliffs, all of which rise or fall straight up and down. A tree trunk is an example of a vertical line in nature, running straight up and down.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.