Surface Area of Cuboid:
Have you ever thought about the geometry behind everyday objects like bricks, packaging boxes, or even your favorite board games? These familiar items share a common shape:
Cuboid
.
But what if you were asked to calculate the exact amount of material needed to cover one completely?
That’s where understanding the surface area of a cuboid becomes essential. In this blog, we will explore the concept of surface area in detail, including its definition, formula, derivation, and more.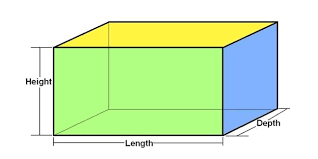
What is the Surface Area of Cuboid?
The surface area of a cuboid is the total area covered by all its rectangular faces. Since a cuboid is a three-dimensional figure, its surface area depends on its
length (l)
,
breadth (b)
, and
height (h)
.
It is measured in square units, such as cm
2
or m
2
. The calculation involves summing the areas of either all six faces (total surface area) or just the four vertical faces (lateral surface area).
Surface Area of Cuboid Formula
A cuboid has two types of surface areas. The type of surface area calculated depends on the requirement. Let’s know the formula for each type of surface re of cuboid:
Total Surface Area of Cuboid
The total surface area of a cuboid includes all six faces (top, bottom, and four vertical sides). For example, if you want to calculate the fabric required to cover a cuboid-shaped sofa completely, you would compute the total surface area.
Lateral Surface Area of Cuboid
The lateral surface area of a cuboid includes only the four vertical sides, excluding the top and bottom faces. For instance, if you need to paint the walls of a cuboid-shaped room without including the floor and ceiling, you would calculate the lateral surface area.
The formulas for both types of surface areas are:
Lateral Surface Area (LSA) =
2h(l+b)
Total Surface Area (TSA) =
2
(lb+bh+lh)
Where:
-
l: Length of the cuboid
-
b: Breadth of the cuboid
-
h: Height of the cuboid
|
Surface Area of Cuboid Formula
Lateral Surface Area (LSA) =
2h(l+b)
Total Surface Area (TSA) =
2
(lb+bh+lh)
|
[video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/Curious-Jr-Ad-3-1-1.mp4"][/video]
Surface Area of Cuboid Formula Derivation
Let’s now understand the derivation of each type of surface
a
re
a
of cuboid:
Total Surface Area
of Cuboid Formula Derivation
As discussed above, the total surface area of a cuboid is calculated by summing the areas of all six rectangular faces. If we denote the length of the cuboid as
l
, the breadth as
b
, and the height as
h
, we can determine the total surface area systematically.
Step-by-Step Calculation:
Front and Back Faces
: Each face has an area of
l×h
and there are two such faces.
Area of front and back faces = 2×(l×h)
Upper and Lower Faces
: Each face has an area of
l×b,
and there are two such faces.
Area of upper and lower faces = 2×(l×b)
Left and Right Faces
: Each face has an area of
b×h
, and there are two such faces.
Area of left and right faces=2×(b×h)
TSA=2(lh)+2(lb)+2(bh)
Factorizing the expression:
TSA=2×(lh+lb+bh)
Thus, the
total surface area
of a cuboid is 2(lh+lb+bh) square
units.
Lateral Surface Area of Cuboid
Derivation
The
lateral surface area (LSA)
of a cuboid represents the total area of its vertical faces, excluding the top and bottom faces. It is useful when calculating the area of the sides only, such as when painting the walls of a cuboid-shaped room without including the ceiling and floor.
The lateral surface area (LSA) of a cuboid includes only the four vertical faces (front, back, left, and right), excluding the top and bottom faces.
Step-by-Step Calculation:
Front and Back Faces
:
2×(l×h)
Left and Right Faces
:
2×(b×h)
Adding these together:
LSA = 2(lh)+2(bh)
Factorizing the expression:
LSA = 2×h(l+b)
Thus, the
lateral surface area
of a cuboid is 2h(l+b) square
units.
[video width="1920" height="1080" mp4="https://www.pw.live/exams/wp-content/uploads/2024/12/curious-jr.mp4"][/video]
How to Find the Surface Area of a Cuboid?
To find the surface area of a cuboid, follow these steps:
Step 1: Identify the Dimensions
-
Measure or note the
length (l)
,
breadth (b)
, and
height (h)
of the cuboid.
-
Ensure the dimensions are in the same units (e.g., all in meters or centimeters).
Step 2: Determine the Type of Surface Area
Decide whether you need:
-
Total Surface Area (TSA):
The area of all six faces of the cuboid.
-
Lateral Surface Area (LSA):
The area of the four vertical faces, excluding the top and bottom.
Step 3: Use the Appropriate Formula
For Total Surface Area (TSA) = 2 (lb+bh+lh),
-
lb: Area of the base or top face.
-
bh: Area of the front or back face.
-
lh: Area of the side faces.
For
Lateral Surface Area = 2h(l+b)
-
l+b: Perimeter of the base.
-
h: Height of the cuboid.
Step 4: Plug in the Dimensions
Substitute the values of l, b, and h into the chosen formula.
Step 5: Simplify the Expression
Perform the necessary arithmetic operations (multiplication and addition) to calculate the surface area.
Step 6: Add the Correct Units
Since the surface area is a two-dimensional measurement, express the result in square units (e.g., cm
2
, m
2
)
Let's understand the above steps with an example below:
Given:
l = 5 m, b = 4 m, h = 3 m
Find the TSA:
TSA = 2(lb+bh+lh)
Substitute the values:
TSA = 2(5 × 4 + 4 × 3 + 5 × 3)
TSA = 2(20 +12 + 15)
TSA = 2 × 47
TSA = 94 m
2
Find the LSA:
LSA = 2h(l+b)
Substitute the values:
LSA = 2 × 3(5 + 4)
LSA = 2 × 3 × 9 = 54 m
2
Surface Area of Cuboid
Solved Examples
Example 1: Determine the lateral surface area of a cuboid if its length, breadth, and height are 18 cm, 9 cm, and 14 cm, respectively.
Solution
:
Given:
-
Length (l) = 18 cm
-
Breadth (b) = 9 cm
-
Height (h) = 14 cm
Lateral surface area formula:
LSA = 2h(l + b)
Substitute the values:
LSA = 2 × 14(18 + 9)
LSA =28 × 27
LSA = 756 sq. cm
Answer
: The lateral surface area is
756 sq. cm
.
Example 2: Calculate the total surface area of a cuboid with dimensions: length = 24 cm, breadth = 16 cm, and height = 12 cm.
Solution
:
Given:
-
Length (l) = 24 cm
-
Breadth (b) = 16 cm
-
Height (h) = 12 cm
Total surface area formula:
TSA = 2(lb + bh + lh)
Substitute the values:
TSA = 2[(24 × 16) + (16 × 12)+(24 × 12)]
TSA = 2 [384 + 192 + 288]
TSA = 2 × 864
TSA = 1728sq. cm
Answer
: The total surface area is
1728 sq. cm
.
Example 3: Find the height of a cuboid whose lateral surface area is 504 sq. cm, with length = 14 cm and breadth = 7 cm.
Solution
:
Given:
-
Length (l) = 14 cm
-
Breadth (b) = 7 cm
-
Lateral surface area (LSA) = 504 sq. cm
Lateral surface area formula:
LSA = 2h(l+b)
Substitute the values:
504 = 2h(14+7)
504 = 2h×21 h
504 = 42h
h = 504/ 42
h =12cm
Therefore, the height of the cuboid is 12 cm.
Example 4: Calculate the length of a cuboid whose lateral surface area is 864 sq. cm, breadth = 10 cm, and height = 18 cm.
Solution
:
Given:
-
Breadth (b) = 10 cm
-
Height (h) = 18 cm
-
Lateral surface area (LSA) = 864 sq. cm
Lateral surface area formula:
LSA = 2h(l+b)
Substitute the values:
864 = 2×18(l+10)
864 = 36 (l + 10)
864 = 36(l + 10)
l +10 = 864/36 = 24
l = 24 −10 = 14 cm
Therefore,
the length of a cuboid is
14 cm
.
