
Calculus , a pivotal branch of mathematics, is concerned with the concepts of rate of change and accumulation. Its foundation rests on two core principles: derivatives and integrals.
Derivatives, in essence, quantify how rapidly a function changes at a specific point, offering insight into the function's behavior at that precise location.
Conversely, integrals serve as a means to measure the area beneath a function's curve, aggregating discrete values across a defined interval.
Often dubbed infinitesimal calculus or "the calculus of infinitesimals," calculus explores the realm of infinitesimal numbers—values that are exceedingly close to, but not precisely, zero. Classical calculus, in general, delves into the study of continuous transformations in functions.
What is Calculus?
Calculus is a mathematical discipline that encompasses key concepts such as differentiation, integration, limits, functions, and more. It was pioneered by luminaries like Newton and Leibniz.
In essence, calculus serves as a foundational tool in mathematical modeling, aiding in the quest for optimal solutions and providing insights into the relationships between values governed by functions. Calculus can be broadly categorized into two distinct branches:
Differential Calculus: This branch focuses on the study of rates of change and slopes of functions, allowing us to analyze how functions evolve and behave locally.
Integral Calculus: Integral calculus, on the other hand, is concerned with accumulation and the computation of areas under curves. It helps us understand the cumulative effects of changing quantities over intervals.
Together, these branches of calculus provide a powerful framework for solving a wide range of mathematical and real-world problems.
Differential calculus and integral calculus collectively lay the groundwork for the advanced branch of mathematics known as "Analysis." This field delves into the consequences of infinitesimal changes in the dependent variable as it approaches zero, examining their impact on the overall behavior of the function.
Calculus Topics
Calculus topics are typically categorized into various levels of complexity, including:
Precalculus: This foundational level introduces essential mathematical concepts and skills needed as prerequisites for calculus. It covers algebra, trigonometry, and basic functions to prepare students for more advanced calculus coursework.
Calculus 1: In this initial calculus course, students delve into fundamental concepts such as limits, derivatives, and their applications. It serves as an introduction to the core principles of calculus.
Calculus 2: Building upon the knowledge gained in Calculus 1, this course explores more advanced topics such as integration, techniques of integration, applications of integrals, sequences, and series. It provides a deeper understanding of calculus and its applications.
Precalculus
Precalculus, a mathematical course, encompasses algebra and trigonometry with the primary objective of equipping students for the study of calculus. Within the realm of precalculus, the emphasis is on the exploration of advanced mathematical principles, including functions and quantitative analysis. Key precalculus topics include:
- Functions: Precalculus delves into the comprehensive understanding of functions, their properties, and their graphical representations.
- Inverse Functions: Inverse functions are a focal point, allowing students to investigate how functions reverse their actions and relate inversely to one another.
- Trigonometric Functions: Precalculus incorporates the study of trigonometric functions, laying the foundation for their in-depth examination in higher-level mathematics.
- Complex Numbers: The course introduces complex numbers, expanding the number system to encompass both real and imaginary components.
- Rational Functions: Rational functions are explored, providing insight into the behavior of functions expressed as ratios of polynomials.
These topics collectively prepare students with the necessary mathematical tools and concepts required for advanced calculus studies.
Calculus 1:
In Calculus 1, the primary focus lies on differential calculus and closely related concepts such as limits and continuity. This course covers a range of fundamental topics, including:
- Limits: Students explore the concept of limits, which serve as the foundation for understanding how functions behave as they approach specific values.
- Derivatives: Calculus 1 delves into derivatives, examining how functions change at individual points and introducing techniques for calculating them.
- Applications of Derivatives: This part of the course applies derivatives to real-world scenarios, allowing students to analyze rates of change in various contexts.
- Integrals: An introduction to integrals is provided, highlighting their role in calculating accumulated quantities and area under curves.
Calculus 2:
Calculus 2 builds upon the mathematical study of change introduced in Calculus 1. Key topics covered in this course include:
- Differential Equations: Students delve into the realm of differential equations, a powerful tool for modeling dynamic processes.
- Sequences and Series: This part of the course focuses on sequences and series, investigating the convergence and divergence of mathematical sequences.
- Application of Integrals: Further applications of integrals are explored, broadening the understanding of how integrals are used to calculate quantities.
- Trapezoidal Rule and Simpson's Rule: Techniques like the Trapezoidal Rule and Simpson's Rule are introduced as methods for approximating definite integrals with numerical precision.
Calculus 2 extends the study of calculus into more advanced and diverse mathematical topics, continuing to build upon the foundation laid in Calculus 1.
Also Check – Line and Angles Formula
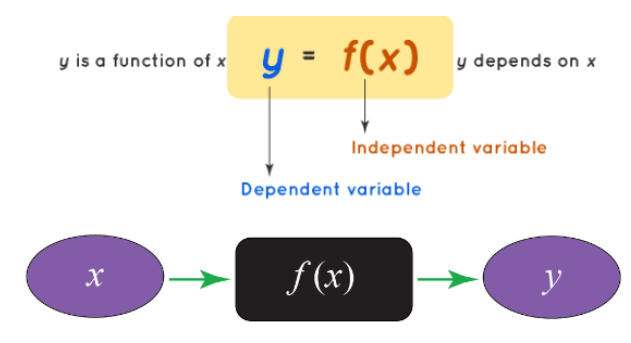
Functions in Calculus
In the realm of calculus, functions serve as a way to depict the relationship between two variables: the independent variable and the dependent variable. To illustrate this concept, let's examine the following diagram:
[Diagram illustrating the concept of a function in calculus]
Within this framework, we have an INPUT, a function, and an OUTPUT. For instance, let's consider the task of making a pizza, which involves several essential ingredients:
- Pizza Base
- Pizza Sauce
- Cheese
- Seasoning
In the context of calculus, this real-life example can be represented as a function, as detailed below:
[Explanation of how the pizza-making process can be represented as a function]
Within this framework, we have three essential components: an INPUT, a function, and an OUTPUT. To illustrate this concept, let's consider the preparation of a pizza as a practical example. In this case, the necessary ingredients include:
- Pizza Base
- Pizza Sauce
- Cheese
- Seasoning
We can interpret this real-life scenario by structuring it as a function, as elucidated below:
Differential Calculus
Differential calculus is primarily concerned with addressing the challenge of determining how a function's rate of change relates to other variables. Derivatives are employed to ascertain optimal solutions by calculating the maximum and minimum values of a function. This branch of mathematics aids in the examination of the limit of a quotient, involving variables such as x and y, functions denoted as f(x), and the associated variations in x and y.
In this context, the notations "dy" and "dx" are referred to as differentials. The systematic approach used to compute derivatives is known as differentiation. When expressing the derivative of a function "y" with respect to variable "x," it is represented as "dy/dx" or "f’(x)."
Limits:
Limits play a crucial role in measuring how close a function gets to a specific value or approaches a particular term. Limits are typically expressed using the limit formula:
lim(x → c) f(x) = A
This expression is read as "the limit of f of x as x approaches c equals A."
Derivatives:
Derivatives provide a means to represent the instantaneous rate of change of a quantity with respect to another. The derivative of a function is symbolized as:
lim(h → 0) [f(x + h) − f(x)]/h = A
Continuity:
In the context of continuity, a function f(x) is considered continuous at a specific point x = a if it satisfies the following three conditions:
f(a) is defined.
lim(x → a) f(x) exists.
lim(x → a) f(x) = f(a).
Continuity and Differentiability:
A function is always continuous if it is differentiable at any given point. However, it's important to note that the reverse statement is not always true; that is, a continuous function may not necessarily be differentiable everywhere.
Also Check – Congruence of triangles formula
Integral Calculus
Integral calculus is a branch of mathematics that deals with the accumulation of quantities and the calculation of areas under curves. It is the counterpart to differential calculus, which focuses on rates of change and derivatives. In integral calculus, the primary concept is the integral, which represents the process of finding the total or accumulated effect of continuously changing quantities.
Here are some key aspects of integral calculus:
- Definite and Indefinite Integrals: Integrals are broadly categorized into definite and indefinite integrals. The definite integral calculates the net accumulation of a quantity over a specific interval, giving a single numerical value. The indefinite integral, on the other hand, provides a family of functions (antiderivatives) that, when differentiated, yield the original function.
- The Integral Symbol: The integral is denoted by the elongated "S" symbol, which represents the process of integration. The function to be integrated is placed within this symbol, and the limits of integration are indicated as subscripts and superscripts.
- Applications: Integral calculus has numerous applications in various fields. It is used to calculate areas, volumes, work done by a force, and other physical quantities. It is also fundamental in probability theory, where it helps calculate probabilities by finding the area under probability density curves.
- Techniques of Integration: There are various techniques for finding integrals, such as substitution, integration by parts, partial fractions, and trigonometric identities. These techniques are employed to solve a wide range of integral problems.
Integral calculus is a powerful mathematical tool with wide-ranging applications in science, engineering, economics, and many other disciplines. It provides a way to understand and quantify the accumulation of quantities and has played a pivotal role in advancing our understanding of the physical world.
Integral calculus revolves around the study of integrals and their associated properties. It serves various purposes, including:
Determining a function (f) from its derivative (f').
Calculating the area beneath a curve for any given function.
Integration:
Integration is the converse process of differentiation. While differentiation divides a whole into smaller parts, integration aggregates these smaller parts to form a complete whole. Its primary application is in the calculation of areas.
Indefinite Integral:
The indefinite integral lacks specific boundaries, meaning it does not have upper and lower limits defined. Consequently, the result of an indefinite integral always includes a constant value (C). This is denoted as:
∫ f(x) dx = F(x) + C, where F'(x) = f(x)
Definite Integral:
In contrast, the definite integral involves precise boundaries or limits for function calculation. It specifies upper and lower limits for the independent variable of a function. Mathematically, the definite integral is represented as:
∫[a to b] f(x) · dx = F(x)
Also Check – Line and Angles Formula
Calculus Formula
Calculus formulas encompass a wide range of mathematical tools and concepts. They can be categorized into six main groups, each serving a specific purpose. These six categories include limits, differentiation, integration, definite integrals, applications of differentiation, and differential equations.
Limits Formulas
Limits formulas are instrumental in approximating the limit of a function at a specific point. Here are some key limits formulas:
lim(x → a) (x^n - a^n) / (x - a) = na^(n-1)
lim(x → 0) (sin x) / x = 1
lim(x → 0) (tan x) / x = 1
lim(x → 0) (e^x - 1) / x = 1
lim(x → 0) (a^x - 1) / x = ln(a)
lim(x → ∞) (1 + (1/x))^x = e
lim(x → 0) (1 + x)^(1/x) = e
lim(x → 0) (1 + (a/x))^x = e^a
These limits formulas are essential tools for understanding the behavior of functions as they approach certain values or conditions, aiding in various mathematical and scientific calculations.
Differentiation Formulas
Differentiation formulas are applicable to a wide range of mathematical expressions, including basic algebraic functions, trigonometric ratios, inverse trigonometry, and exponential terms. Here are some essential differentiation formulas:
d/dx (x^n) = nx^(n-1)
d/dx (Constant) = 0
d/dx (e^x) = e^x
d/dx (a^x) = a^x · ln(a)
d/dx (ln(x)) = 1/x
d/dx (sin(x)) = cos(x)
d/dx (cos(x)) = -sin(x)
d/dx (tan(x)) = sec^2(x)
d/dx (cot(x)) = -csc^2(x)
d/dx (sec(x)) = sec(x) · tan(x)
d/dx (csc(x)) = -csc(x) · cot(x)
Integration Formulas
Integration formulas are complementary to differentiation formulas and can be derived from them. They are used to calculate antiderivatives. Here are some key integration formulas:
∫ x^n dx = (x^(n+1))/(n+1) + C
∫ 1 dx = x + C
∫ e^x dx = e^x + C
∫ (1/x) dx = ln |x| + C
∫ a^x dx = (a^x)/(ln(a)) + C
∫ cos(x) dx = sin(x) + C
∫ sin(x) dx = -cos(x) + C
∫ sec^2(x) dx = tan(x) + C
∫ csc^2(x) dx = -cot(x) + C
∫ sec(x)tan(x) dx = sec(x) + C
∫ csc(x)cot(x) dx = -csc(x) + C
Definite Integrals Formulas
Definite integrals include limits and are useful for finding the area within specified bounds. Here are some key definite integrals formulas:
∫[a to b] f'(x) dx = f(b) - f(a) (Fundamental Theorem of Calculus)
∫[a to b] f(x) dx = ∫[a to b] f(t) dt
∫[a to b] f(x) dx = -∫[b to a] f(x) dx
∫[a to b] f(x) dx = ∫[a to c] f(x) dx + ∫[c to b] f(x) dx
∫[a to 0] f(x) dx = ∫[a to 0] f(a - x) dx
∫[-a to a] f(x) dx = 2∫[0 to a] f(x) dx (for even functions)
∫[-a to a] f(x) dx = 0 (for odd functions)
Application of Differentiation Formulas
Certainly, differentiation formulas find numerous applications across various fields. Here are some common applications of differentiation formulas:
Physics and Engineering:
- Motion Analysis: Derivatives are used to calculate velocities and accelerations, making them invaluable in physics to analyze the motion of objects.
- Electric Circuits: In electrical engineering, derivatives help model and analyze circuits with changing voltage and current.
- Mechanics: Derivatives are crucial in mechanical engineering for analyzing forces, stresses, and deformations in structures and machines.
Economics:
Marginal Analysis: In economics, derivatives are used to determine marginal costs, marginal revenue, and marginal utility, aiding in decision-making and optimization.
Biology:
Population Growth: Derivatives are employed to model and study population growth and decay in biological systems.
Chemistry:
Rate of Reactions: Derivatives help determine reaction rates in chemical kinetics, allowing chemists to study the speed of reactions.
Computer Science:
Algorithm Analysis: In computer science, derivatives assist in analyzing algorithm efficiency and runtime, aiding in algorithm design and optimization.
Finance:
Risk Assessment: Derivatives are used to calculate financial risk, such as in the computation of derivatives like options and futures contracts.
Medicine:
Drug Dosage: In pharmacology, derivatives play a role in determining optimal drug dosages based on how the concentration of a drug changes in the body over time.
Environmental Science:
Ecosystem Modeling: Derivatives help create mathematical models for studying and predicting changes in ecosystems.
Statistics:
Regression Analysis: Derivatives are employed in regression analysis to find the best-fit curve for a set of data points.
Geometry:
Curvature: Derivatives are used to calculate the curvature of curves and surfaces in geometry, helping in the study of shapes and surfaces.
These are just a few examples, and differentiation formulas have applications in virtually every field of science, engineering, and mathematics where the rate of change or the slope of a curve is of interest. They are fundamental tools for understanding and solving real-world problems.
Applications of Calculus
Calculus stands as a pivotal mathematical discipline with a multitude of practical applications, facilitating:
- Optimization and Prediction: It aids in the analysis of systems to uncover optimal solutions and predict the future state of functions under varying conditions.
- Real-Life Problem Solving: The concepts of calculus are widely employed in solving diverse real-world challenges, including the computation of complex shapes' areas, data analysis in surveys, vehicle safety assessments, financial planning, credit card transaction records, and the study of dynamic system behaviors affecting our daily lives.
- Interdisciplinary Utility: Calculus serves as a universal language, bridging disciplines like economics, biology, architecture, medicine, and statistics. For instance, architects and engineers harness calculus to determine the dimensions and structural integrity of constructions.
- Modeling Complex Phenomena: Calculus is instrumental in modeling intricate phenomena such as birth and death rates, radioactive decay, chemical reaction kinetics, heat and light diffusion, object motion, and electrical circuit behavior, among others.
In essence, calculus is a versatile tool that finds application across a spectrum of fields, enabling professionals and researchers to understand, analyze, and make informed decisions about a wide array of dynamic processes and systems.
Examples
Example 1: Given f(y) = y^2 and g(y) = e^y. To find h′(y) for h(y) = f(g(y)) using the chain rule:
Solution: We have f'(y) = 2y and g'(y) = e^y.
Using the chain rule, h'(y) = f'(g(y)) * g'(y).
Substituting the values, h'(y) = 2(e^y) * e^y = 2e^(2y).
Example 2: For y = f(x) = 1/(1 + x^2), find f(0), f(-1), and f(√2).
Solution: Calculate f(x) for different values of x:
f(0) = 1 / (1 + 0^2) = 1 / 1 = 1.
f(-1) = 1 / (1 + (-1)^2) = 1 / 2.
f(√2) = 1 / (1 + (√2)^2) = 1 / 3.
Example 3: Find the slope of the tangent to the curve y = 2x^2 + 3x + 1 at the point (-1, 0).
Solution: The derivative of the curve is dy/dx = 4x + 3. At the point (-1, 0), the slope is given by m = 4(-1) + 3 = -1.
Example 4: Differentiate x tan x.
Solution: Using the product rule, differentiate x tan x:
d/dx (x tan x) = x * d/dx (tan x) + tan x * d/dx (x).
Using calculus formulas, d/dx (x tan x) = x * sec^2(x) + tan x * 1 = x sec^2(x) + tan x.
Calculus Formula FAQs
Q1. What is calculus, and why is it important?
Q2. What are differentiation and integration in calculus?
Q3. What is the chain rule in calculus?
Q4. What are the basic differentiation formulas?
Q5. How do you find the derivative of a product of two functions?










