Congruence Of Triangle Formula - SSS, SAS, ASA, & RHS

Congruence Of Triangle Formula: The congruence between two or more triangles is contingent upon the measurements of their angles and sides. The size of a triangle is determined by its three sides, while its shape is dictated by the arrangement of its three angles. When pairs of corresponding sides and corresponding angles in two triangles are equivalent, the triangles are deemed congruent. This indicates that they possess identical shape and dimensions. There exist various conditions under which triangle congruence holds, and we will explore them comprehensively.

Understanding Triangle Congruence

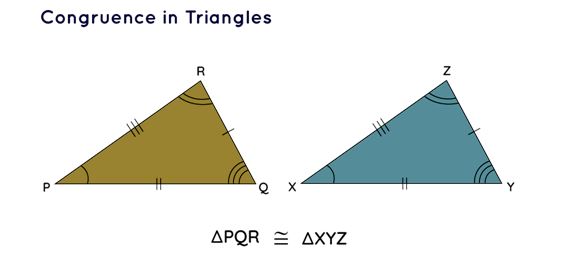
If the three angles and the three sides of one triangle coincide with the corresponding angles and sides of another triangle, the two triangles are referred to as congruent. In the context of triangles Δ PQR and Δ XYZ illustrated below, it can be discerned that PQ equals XY, PR equals XZ, and QR equals YZ. Additionally, ∠ P matches ∠ X, ∠ Q aligns with ∠ Y, and ∠ R corresponds to ∠ Z. Consequently, it is valid to assert that Δ PQR is congruent to Δ XYZ.

for triangles to be considered congruent, they must possess identical dimensions and configurations. These two triangles must align precisely when placed on top of each other. However, if we subject a triangle to rotation, reflection, and/or translation, its orientation or visual manifestation might alter. In such instances, it becomes necessary to pinpoint the six components of a triangle alongside their corresponding counterparts in the alternate triangle. Let's contemplate the scenario of Δ ABC and Δ PQR depicted below.

Also Check - Rational Numbers

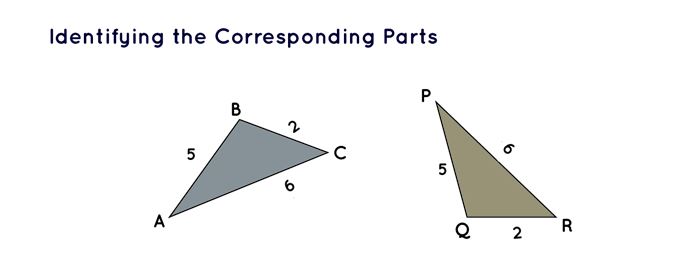
Thus, on identifying the corresponding parts of the given triangles, we can confirm that Δ ABC ≅ ΔPQR.

Conditions of Congruence in Triangles

When two triangles possess identical dimensions and identical configurations, they are considered congruent. It is not always essential to establish equivalence in all six corresponding components of both triangles to ascertain their congruence. Research and empirical investigations have revealed five specific conditions that govern the congruence of two triangles.

here are various methods to prove congruency among triangles. The methods which are used to prove congruency between two triangles are:

• SSS Criteria: Side-Side-Side
• SAS Criteria: Side-Angle-Side
• ASA Criteria: Angle-Side-Angle
• AAS Criteria: Angle-Angle-Side
• RHS Criteria: Right angle- Hypotenuse-Side

Also Check - Algebra Formulas

Properties of Congruent Triangles

Various properties of congruent triangles are

• Congruent Triangles are mirror images of each other.
• Congruent Triangles perfectly overlap each other if arranged in the proper orientation.
• Corresponding parts of Congruent Triangles are equal.
• Congruent Triangles have the same area.

Also Check - Comparing Quantities Formula

SSS Criterion for Congruence

The acronym SSS signifies the Side-Side-Side criterion for congruence. According to this criterion, two triangles are deemed congruent when the lengths of the three sides of one triangle correspond precisely to the lengths of the corresponding sides of another triangle.

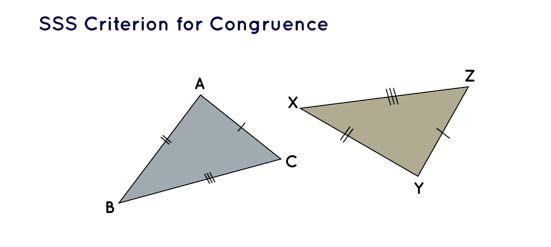
The criterion for Congruence based on SSS

In the scenario where Δ BAC ≅ Δ XYZ applies within the framework of the SSS criterion, it naturally follows that the three angles of Δ BAC are inherently identical to the corresponding angles within Δ XYZ.

SAS Criterion for Congruence

The abbreviation SAS signifies the Side-Angle-Side criterion for establishing congruence. According to this criterion, two triangles achieve congruence when both the lengths of two sides and the measure of the included angle of one triangle match the corresponding measurements of two sides and the included angle of another triangle.

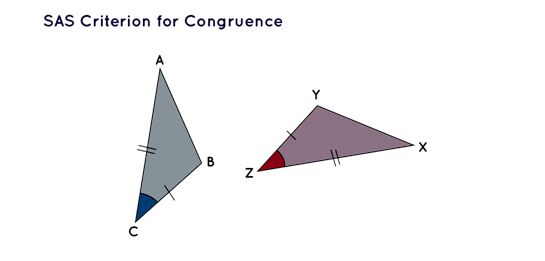
The criterion for Congruence based on SAS

In the context where Δ ABC ≅ Δ XYZ holds true within the framework of the SAS criterion, it logically implies that the third side (AB) and the other two angles within Δ ABC will inherently align in equivalence with the corresponding side (XY) and angles within Δ XYZ.

ASA Criterion for Congruence

The acronym ASA represents the Angle-Side-Angle criterion used to establish congruence. According to this criterion, two triangles are considered congruent when two angles and the side between them in one triangle coincide in measurement with the corresponding angles and the associated side in another triangle.

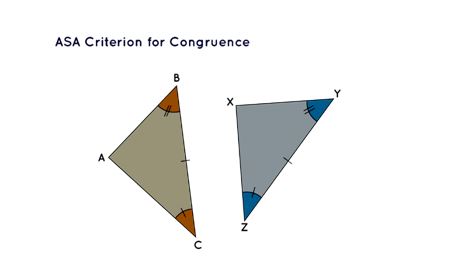
The criterion for Congruence based on ASA

In the circumstance where Δ ABC ≅ Δ XYZ is applicable following the ASA criterion, it logically indicates that the third angle ( ∠ BAC) and the other two sides within Δ ABC will inherently match the corresponding angle ( ∠ YXZ) and the sides within Δ XYZ.

AAS Criterion for Congruence

The abbreviation AAS designates the Angle-Angle-Side criterion, a standard for affirming congruence. In accordance with this criterion, two triangles are deemed congruent when any two angles and the side not in between them of one triangle mirror the corresponding angles and the parallel side of another triangle.

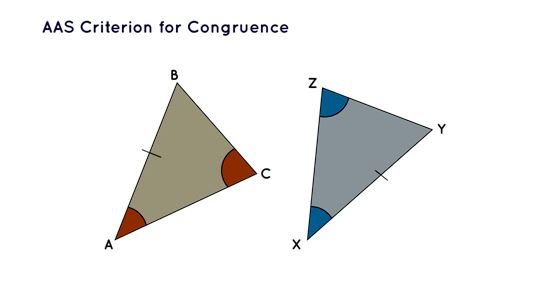
The criterion for Congruence based on AAS

In the event where Δ ABC ≅ Δ XYZ is verified under the AAS criterion, it logically entails that the third angle ( ∠ ABC) and the other two sides (AC and BC) within Δ ABC inherently match the corresponding angle ( ∠ XYZ) and sides (XZ and YZ) within Δ XYZ.

RHS Criterion for Congruence

The RHS abbreviation represents the right angle-hypotenuse-side congruence criterion utilized to determine congruence. As per this criterion, two right-angled triangles achieve congruence when the hypotenuse and one of the sides in one triangle match the hypotenuse and the corresponding side in another right-angled triangle.

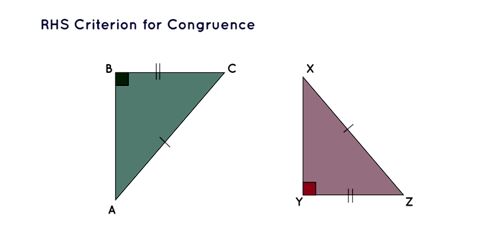
The criterion for Congruence based on RHS

In the context where Δ ABC ≅ Δ XYZ holds true following the RHS criterion, it naturally follows that the third side (AB) and the other two angles within Δ ABC will inherently align in equivalence with the corresponding side (XY) and angles within Δ XYZ.

Download Pdf Congruence Of Triangle Formula

Points to Remember

• To ascertain the congruence between two triangles, five distinct conditions come into play. These conditions comprise the SSS, SAS, ASA, AAS, and RHS criteria.
• However, it's important to note that possessing identical corresponding angles in two triangles does not necessarily lead to congruence. This is due to the potential scenario where one triangle is an expanded replica of the other. Consequently, an AAA criterion for congruence does not exist.
• The symbol ( ≅ ) is used to denote congruence.
• In cases of triangle congruence, not only are the perimeters but also the areas of the two triangles identical if they are congruent.