Diagonal of A Square Formula: Definition, Properties, Examples

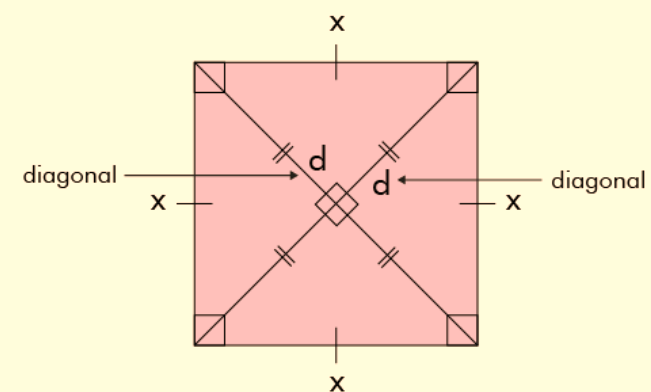
The Diagonal of a Square refers to the line segment that connects two opposite vertices (corners) of the square. In other words, it is a straight line that cuts through the interior of the square, connecting two non-adjacent corners.

What is the Diagonal of a Square?

Some important properties of the diagonals of a square:

Congruence: The diagonals of a square are congruent, which means they have the same length. This is because a square has all its sides equal, and the diagonals connect opposite vertices.

Perpendicular Bisectors: The diagonals of a square are also perpendicular bisectors of each other. This means that they intersect at a 90-degree (right) angle, and they divide each other into two equal segments. This property holds true for all squares.

Isosceles Right-Angled Triangles: Each diagonal of a square divides the square into two congruent isosceles right-angled triangles. These triangles have two sides of equal length, which are the diagonals themselves, and they each have a right angle (90 degrees). This property is helpful for various geometric calculations involving squares.

Understanding these properties of square diagonals is essential when working with squares in geometry and various applications, as it simplifies calculations and provides insights into their geometric relationships.

What is the Formula for the Diagonal of a Square?

The formula to calculate the length of the diagonal of a square with side length "s" is:

Diagonal (d) = s√2

Where:

"d" represents the length of the diagonal.

"s" represents the side length of the square.

√2 denotes the square root of 2.

This formula allows you to find the length of the diagonal when you know the side length of the square. The diagonal is an important geometric concept and property of squares, and it is commonly used in various mathematical and engineering calculations.

Also Check – Line and Angles Formula

Derivation of the Diagonal of a Square Formula

To derive the formula for the diagonal of a square, you can use the Pythagorean theorem. The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. In the case of a square, the diagonal forms the hypotenuse of two congruent right triangles.

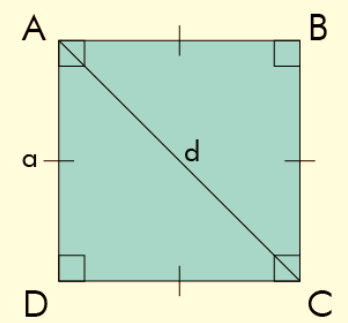
Let's start with a square with side length "a" and draw its diagonal "d":

In each right triangle, one side has a length of "a" (half of a side of the square), another side has a length of "a" (the other half of the side of the square), and the diagonal "d" is the hypotenuse.

Using the Pythagorean theorem for one of these triangles:

(squared hypotenuse) = (squared side) + (squared side)

d ² = a ² + a ²

d ² = 2a ²

Now, take the square root of both sides to solve for "d":

d = √(2a ² )

d = s√2

So, the formula for the length of the diagonal of a square, given its side length "s," is:

Diagonal (d) = s√2

This is the derived formula for the diagonal of a square using the Pythagorean theorem.

Also Check – Congruence of triangles formula

Area of Square by Applying Formula for the Diagonal

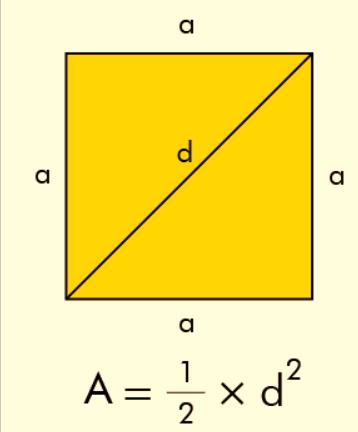
The formula for finding the area of a square in terms of its diagonal (d) is as follows:

Area (A) = (1/2) * (d ² )

Where:

"A" represents the area of the square.

"d" represents the length of the diagonal.

However, it's important to note that the most common and straightforward way to calculate the area of a square is by using the formula based on its side length (s):

Area (A) = s2

This formula simply involves squaring the length of one of the sides. Using the diagonal formula to find the area is less common and may involve extra calculations, especially if you don't already know the diagonal length.

Also Check – Line and Angles Formula

Diagonal of a Square Formula Examples

Example 1: Given a square with a side length of 15 inches, we can determine the length of its diagonal using the formula for the diagonal of a square:

Solution:

Diagonal d = a √ 2

Substituting the value of the side length (a = 15 inches):

d = 15 √ 2

Now, calculate the diagonal length:

d ≈ 15 inches * 1.414 (rounded to three decimal places for √2)

d ≈ 21.213 inches (rounded to three decimal places)

So, the length of the diagonal is approximately 21.213 inches.

Example 2: Suppose you have a square cake with a diagonal length of 12 inches, and you wish to determine its area.

Solution 2:

To find the area of a square, you can use the following formula:

Area A = 1/2 × d ²

Now, plug in the value of the diagonal (d = 12 inches):

A = 1/2 × 12 ²

A = 1/2 × 144 square inches

A = 72 square inches

Therefore, the actual size of Paul's birthday cake is 72 square inches.

Example 3: Suppose you have a square-shaped parking lot, and the length of its diagonal is 20 feet. To calculate the area of this parking lot, you can use the formula for the area of a square:

Solution:

Area A = 1/2 × d ²

Now, substitute the given diagonal length (d = 20 feet) into the formula:

A = 1/2 × 20 ²

A = 1/2 × 400 square feet

A = 200 square feet

So, the area of the square-shaped parking lot is 200 square feet.