Inverse Matrix Formula: Examples, Properties, Method

Before delving into the computation of a Inverse Matrix , it's important to establish what a matrix is. A matrix is a structured arrangement of elements organized into rows and columns. Each individual element within the matrix is referred to as an element. The dimensions of a matrix are denoted by the number of rows and columns it possesses. For instance, matrix orders can be expressed as 2 × 2, 2 × 3, 3 × 2, 3 × 3, 4 × 4, and so forth. The process of finding the inverse of a matrix is exclusively applicable to square matrices, those matrices where the number of rows equals the number of columns, such as 2 × 2, 3 × 3, and so on. In simpler terms, the inverse matrix is derived by dividing the adjugate of the given matrix by the determinant of that matrix. In this article, you will gain a comprehensive understanding of what a matrix inverse entails, how to compute it through various methods, explore the properties of inverse matrices, and examine detailed examples.

Matrix Inverse

If you have a non-singular square matrix A, it implies that there exists an n x n matrix A ^-1 , referred to as the inverse matrix of A, with the property:

AA ^-1 = A ^-1 A = I, where I represents the identity matrix.

For a 2 x 2 matrix, the identity matrix is given by:

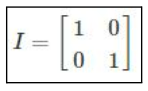
It is important to highlight that to compute the inverse matrix, the square matrix in question must be non-singular, meaning its determinant value is not equal to zero.

Let's consider the square matrix A.

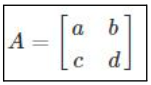
Where a, b, c, and d represents the number.

The determinant of matrix A is represented as ad-bc, and it's crucial for this determinant not to equal zero to enable the existence of an inverse. The process of finding the inverse matrix can be applied to matrices of various dimensions, including 2×2, 3×3, and so on. Calculating the inverse of a 3×3 matrix is relatively more complex compared to finding the inverse of a 2×2 matrix.

Inverse Matrix Method

The inverse of a matrix can be determined using three distinct methods. It's important to note that regardless of the method chosen, all three approaches will yield the same result.

Method 1.

In the same manner, we can compute the inverse of a 3×3 matrix by evaluating the determinant value of the given matrix.

Method 2.

One of the key methods for determining the inverse of a matrix involves a systematic process of calculating minors and cofactors for the elements within the given matrix. Below are the steps to understand this method clearly:

The inverse matrix can be computed using the following equation:

A ^-1 = adj(A) / det(A),

Where adj(A) represents the adjoint of matrix A, and det(A) denotes the determinant of matrix A.

The adjoint of a matrix A, or adj(A), can be derived through the following procedure:

To find the adjoint of matrix A, start by calculating the cofactor matrix for the given matrix. Then, take the transpose of this cofactor matrix.

The cofactor of a matrix, denoted as Cij, can be obtained as:

C _ij = (-1) ^i+j * det(Mij),

Here, Mij signifies the minor matrix resulting from the removal of the ith row and the jth column. It's worth noting that the transpose of the cofactor matrix is also known as the adjoint of matrix A.

This process is applicable to finding the inverse of a 3 x 3 matrix as well. In this case, the initial step is to determine the determinant, followed by the subsequent step – transposition.

Also Check – Derivatives Formula

Method 3.

Determining an Inverse Matrix through Elementary Transformations

Let's consider three matrices: X, A, and B, with the relationship X = AB. To find the inverse of a matrix using elementary transformations, we aim to transform the given matrix into an identity matrix. To learn more about the process of elementary transformations for matrices, you can find additional information here.

If the inverse of matrix A, denoted as A ^-1 , exists, then the process for determining A-1 through elementary row operations involves the following steps:

Express A as IA, where I is the identity matrix of the same order as A.

Apply a series of row operations until an identity matrix is achieved on the left-hand side (LHS). Simultaneously, use the same elementary operations on the right-hand side (RHS) to obtain I = BA. The matrix B on the RHS represents the inverse of matrix A.

To find the inverse of A using column operations, you can similarly express A as IA and apply column operations sequentially until I = AB is obtained, where B is the inverse matrix of A.

Also Check – Factors and Multiples Formula

Inverse of a Matrix Formula

Inverse Matrix 2 x 2 Example

To gain a clearer understanding of this concept, let's examine the following illustration.

Example: Determine the inverse of the matrix A provided below:

Also Check – Integer Formula

Inverse Matrix 3 x 3 Example

Example:

Solution :

Determinant of the given matrix is

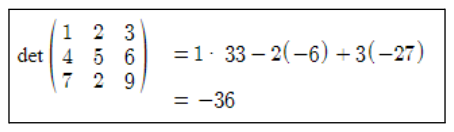
Let us find the minors of the given matrix as given below:

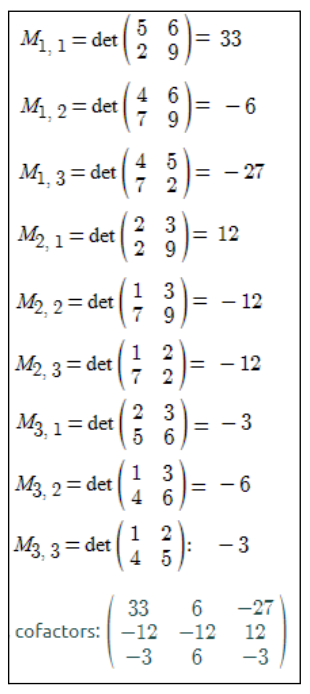
Now, find the adjoint of a matrix by taking the transpose of cofactors of the given matrix.

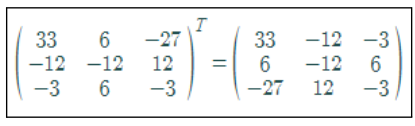
Now,

A ^-1 = (1/|A|) Adj A

Hence, the inverse of the given matrix is:

Properties

Here are some key properties of the inverse matrix, presented in a rephrased manner:

If A is a non-singular matrix, then the inverse of its inverse, (A ^-1 ) ^-1 , is equal to A.

When A and B are non-singular matrices, the product of AB is also non-singular, and the inverse of AB, denoted as (AB) ^-1 , is equal to B ^-1 A ^-1 .

For a non-singular matrix A, the inverse of its transpose, (A ^T ) ^-1 , is equal to the transpose of its inverse, (A ^-1 ) ^T .

For any matrix A with an inverse, denoted as A ^-1 , the product of A and its inverse, AA ^-1 , is equal to the product of its inverse and itself, A ^-1A , both of which result in the identity matrix In, where n represents the order of the matrices involved.