
Factors and Multiples Formula: In mathematics, factors and multiples are two fundamental concepts that go hand in hand. Factors are numbers that evenly divide another number, while multiples are numbers that result from multiplying one number by another. In this article, we will examine the meanings of factors and multiples, provide examples, and emphazise the important differences between them.
 Also Check -
Factorization Formula
Also Check -
Factorization Formula
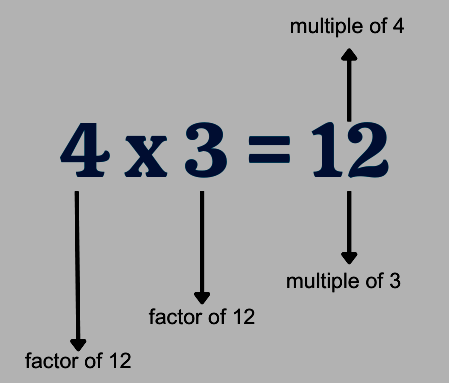
Factor Definition
Factors are numbers that can divide another number without leaving a remainder. In simpler terms, if one number (the divisor) can evenly divide another number (the dividend), then the divisor is considered a factor of the dividend. Every number has at least two factors: 1 and itself.
For example, in the case of the number 24, both 4 and 6 are factors because they divide 24 evenly, resulting in a quotient with no remainder. Thus, 24 has factors of 1, 24, 4, and 6, in addition to 2, 3, 8, and 12, all of which also evenly divide 24.
Prime numbers, on the other hand, have only two factors: 1 and the number itself. For instance, 2 is a prime number because it can only be divided by 1 and 2.
Also Check - Logarithm FormulaMultiples Definition
Multiples of a number are the products of that number and other natural numbers. You can often find multiples by examining a multiplication table. Here are examples of multiples for various numbers:
Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, and so on. Multiples of 2 are even numbers and end with digits 0, 2, 4, 6, or 8.
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, and so on.
Multiples of 5: 5, 10, 15, 20, 25, and so on. Every multiple of 5 ends with either 0 or 5.
In essence, multiples are the results of multiplying a specific number by various other numbers.
Also Check - Ratio and Proportion FormulaDifference Between Factors and Multiples
| S. No | Factors | Multiples |
| 1 | Factors are exact divisors of the given number. | Multiples are numbers obtained by multiplication. |
| 2 | The number of factors is finite. | The number of multiples is infinite. |
| 3 | The operation used to find factors is division. . | The operation used to find multiples is multiplication |
| 4 | The outcomes of factors are less than or equal to the given number. | The outcomes of multiples are greater than or equal to the given number. |
Factors and Multiples Formula Solved Examples
Example 1: Factors of 20
Factors of 20 are 1, 2, 4, 5, 10, and 20. These numbers evenly divide 20, leaving no remainder.
Example 2: Multiples of 20
Multiples of 20 include 20, 40, 60, 80, 100, 120, and so on. These multiples result from multiplying 20 by different natural numbers.
Example 3: Factors of 15
Factors of 15 are 1, 3, 5, and 15. These numbers can divide 15 evenly without leaving a remainder.
Example 4: Multiples of 7
Multiples of 7 include 7, 14, 21, 28, 35, 42, 49, 56, 63, and so on. Each of these multiples results from multiplying 7 by different natural numbers.
Example 5: Factors of 9
Factors of 9 are 1, 3, and 9. These numbers divide 9 evenly.
Example 6: Multiples of 12
Multiples of 12 comprise 12, 24, 36, 48, 60, 72, 84, 96, 108, and so forth. These multiples are obtained by multiplying 12 by various natural numbers.
Example 7: Factors of 50
Factors of 50 are 1, 2, 5, 10, 25, and 50. Each of these factors can evenly divide 50.
Example 8: Multiples of 6
Multiples of 6 include 6, 12, 18, 24, 30, 36, 42, 48, 54, and so on. These multiples result from the multiplication of 6 by different natural numbers.
Example 9: Factors of 16
Factors of 16 are 1, 2, 4, 8, and 16. These factors can divide 16 evenly.
Example 10: Multiples of 9
Multiples of 9 comprise 9, 18, 27, 36, 45, 54, 63, 72, 81, and so forth. These multiples are the products of multiplying 9 by various natural numbers.
Factors and Multiples Formula FAQs
What are factors and multiples?
How do you find factors of a number?
What are prime numbers?
How do you find multiples of a number?
Is the number of factors finite or infinite?










