What is Relativistic Mass?
Before we dive into the formula, let's grasp the fundamental concept of relativistic mass. In classical physics, mass is considered a constant, meaning an object's mass remains the same regardless of its velocity. However, Einstein's theory of relativity introduced the idea that as an object's speed approaches the speed of light (denoted as 'c'), its mass appears to increase.
The Relativistic Mass Formula
The
Relativistic Mass
Formula allows us to calculate the relativistic mass of an object as it moves at a significant fraction of the speed of light. The formula is as follows:
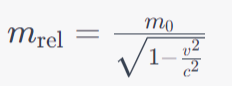
Where:
-
- m
rel
is the relativistic mass.
-
- m
o
is the rest mass of the object (its mass at rest).
-
- v is the velocity of the object.
-
- c is the speed of light in a vacuum (approximately 3 \times 10^8 meters per second).
Also Check -
Net Force Formula
Interpreting the Formula
To understand the implications of the
Relativistic Mass
Formula, let's consider a hypothetical scenario. Imagine a spaceship traveling at a significant fraction of the speed of light. As the spaceship's velocity (v) approaches c, the denominator of the formula approaches zero, causing the relativistic mass (m_{\text{rel}}) to approach infinity. This implies that the amount of energy required to continue accelerating the spaceship also approaches infinity. Therefore, it becomes practically impossible to accelerate an object with mass to the speed of light.
Also Check -
Reynolds Number Formula
Practical Applications
The
Relativistic Mass
Formula finds applications in various branches of physics, particularly in particle physics and astrophysics. It helps scientists understand the behavior of particles traveling at high speeds, such as those in particle accelerators or celestial objects like stars and galaxies.
-
Particle Physics:
- Description:
Particle physics involves the study of subatomic particles and their interactions. The
Relativistic Mass
Formula plays a critical role in this field when particles are accelerated to near the speed of light in particle accelerators like the Large Hadron Collider (LHC). As particles gain relativistic mass at high speeds, it affects their behavior and allows scientists to study fundamental particles and forces in the universe.
-
Nuclear Physics:
- Description:
In nuclear physics, the
Relativistic Mass
Formula is essential for understanding the behavior of particles within atomic nuclei. It is particularly relevant when studying nuclear reactions, fission, and fusion. The relativistic effects on the mass of particles involved in these processes are crucial for accurate predictions and modeling.
-
Astrophysics:
- Description:
The formula finds applications in astrophysics, especially when dealing with celestial objects moving at substantial fractions of the speed of light. For example, when studying the behavior of particles in the intense gravitational fields around black holes or the relativistic jets emitted by active galactic nuclei, the Relativistic Mass Formula is used to account for the mass increase due to high velocities.
-
Space Travel and Exploration:
- Description:
In the context of space travel, the
Relativistic Mass
Formula is applied to calculate the energy required for spacecraft to achieve high speeds. As a spacecraft approaches a significant fraction of the speed of light, its relativistic mass increases, leading to greater energy requirements. Understanding these effects is essential for planning missions to distant celestial bodies.
-
Cosmic Rays and High-Energy Particles:
- Description:
Cosmic rays are high-energy particles from space that can impact the Earth's atmosphere. These particles often travel at relativistic speeds. The Relativistic Mass Formula helps scientists determine the energy and behavior of cosmic rays as they interact with the Earth's atmosphere and can even be used to understand the physics of supernova explosions that produce these particles.
Also Check -
Lorentz Factor Formula
-
Special Relativity Experiments:
- Description:
Experiments that test the principles of special relativity, such as the famous Michelson-Morley experiment, rely on the
Relativistic Mass
Formula. This formula helps explain why the speed of light is constant for all observers and why time dilation and length contraction occur at relativistic speeds.
-
GPS and Relativistic Corrections:
- Description:
Global Positioning System (GPS) satellites are equipped with highly accurate atomic clocks. These clocks are affected by the theory of relativity, including the concept of relativistic mass. The formula is used to correct for time dilation effects due to the satellites' orbital velocities, ensuring precise GPS navigation.
-
Particle Accelerators and Collider Physics:
- Description:
Particle accelerators, such as the LHC, accelerate particles to near-light speeds to study their behavior. The
Relativistic Mass
Formula is fundamental in designing and operating these machines. It helps physicists calculate the energy needed to achieve specific collision energies.
