The
net force formula
is a fundamental concept in physics that describes how multiple forces acting on an object combine to produce a single resultant force. This explanation will provide a comprehensive overview of the net force formula, including its definition, mathematical representation, vector nature, and practical applications.
I. Introduction to Net Force
Net Force is a fundamental concept in physics, representing the interaction between two objects or the influence that causes an object to accelerate. When multiple forces act on an object, they combine to create a net force. The net force determines the object's motion, specifically its acceleration, and is critical for understanding how objects move in response to various influences.
II. Definition of Net Force
The net force on an object is defined as the vector sum of all the individual forces acting on that object. Each force has both magnitude and direction, and when these forces are combined, their vector sum yields the net force. Mathematically, the net force (F_textnet) can be expressed as:
F
net
= Σ F_i
Where:
-
- F_net is the net force.
-
- Σ represents the summation symbol, indicating that we are adding up all the individual forces.
-
- F_i represents each individual force acting on the object.
Also Check -
Inductive Reactance Formula
III. Vector Nature of Net Force
It's important to emphasize that force is a vector quantity, meaning it has both magnitude and direction. As a result, when calculating the net force, you must consider both the magnitude and direction of each force involved. To calculate the net force correctly, it's often helpful to break forces down into their components along different axes, typically the x, y, and z axes for three-dimensional problems.
IV. Force Components
In many real-world situations, forces act at angles with respect to the coordinate axes. To calculate the net force, you'll need to determine the force components along each axis. This is done using trigonometry.
Consider a force F acting at an angle 𝛉 to the horizontal axis. You can find the horizontal component (F_x) and the vertical component (F_y) using the following equations:
F_x = F * cos(𝛉)
F_y = F * sin(𝛉)
These components allow you to analyze how the force contributes to motion in each direction.
Also Check -
Gregory Newton Formula
V. Adding Force Vectors
Once you've determined the components of all the forces acting on an object, you can add them to find the net force along each axis. For instance, if you have multiple forces acting in the x-direction (F_x1}, F_x2, etc.) and multiple forces in the y-direction (F_y1}, F_y2}, etc.), you can find the net force in each direction separately:
F
net,x
= Σ F
_
xi
F
net,y
= Σ F
_
yi
VI. Finding the Net Force Vector
To find the overall net force acting on the object, you can combine the net forces along each axis into a single vector. This is typically done using the Pythagorean theorem for the magnitude of the net force (F
net
) and trigonometry for the direction (𝛉_textnet).
The magnitude of the net force is given by:
With these equations, you can determine both the magnitude and direction of the net force acting on the object.
VII. Units of Force
In the International System of Units (SI), the unit of force is the newton (N). One newton is defined as the force required to accelerate a one-kilogram mass by one meter per second squared (1N} = 1 kg} * m/s
2
). Therefore, when calculating the net force, it's essential to ensure that all forces are expressed in newtons if they are not already.
Also Check -
Weight formula
VIII. Practical Applications of Net Force
The concept of net force is fundamental and has numerous practical applications across various fields of science and engineering. Some notable examples include:
-
Mechanics: In classical mechanics, the net force is used to calculate the motion of objects subjected to multiple forces. It helps in understanding the behavior of objects under the influence of gravity, friction, tension, and more.
-
Astronomy: Net force is crucial in celestial mechanics to study the motion of planets, moons, and other celestial bodies in gravitational fields.
-
Engineering: Engineers use the concept of net force when designing structures, analyzing stress and strain in materials, and ensuring the stability of buildings and bridges.
-
Aerospace: In aerospace engineering, understanding net forces is vital for spacecraft and aircraft design, including calculating thrust, lift, and drag forces.
-
Electromagnetism: In the field of electromagnetism, net forces are used to describe how electric and magnetic fields interact with charged particles.
-
Fluid Mechanics: Net forces play a role in fluid dynamics, where they are used to analyze the motion of fluids and their effects on objects submerged in them.
-
Biomechanics: In the study of biomechanics, net forces are used to analyze the forces exerted on the human body during activities such as walking, running, and sports.
IX. Newton's Second Law and Net Force
Newton's Second Law of Motion relates the net force acting on an object to its acceleration and mass. It can be expressed mathematically as:
F net = m * a
Where:
-
- F net is the net force.
-
- m is the mass of the object.
-
- a is the acceleration of the object.
This law implies that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. Therefore, if you know the net force and the mass of an object, you can determine its acceleration, and vice versa.
X. Free-Body Diagrams
To analyze complex situations involving multiple forces, it is often helpful to create free-body diagrams (FBDs). A free-body diagram is a visual representation of an object with all the external forces acting on it shown as vectors. By drawing a free-body diagram, you can systematically analyze the forces and determine the net force more easily.
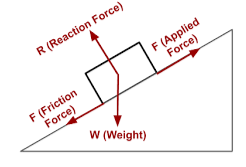
XI. Equilibrium and Net Force
In some cases, the net force acting on an object is zero
. This situation is known as equilibrium, and it occurs when all the forces acting on an object cancel each other out. Mathematically, for an object in equilibrium:
F
net
= 0
In other words, the sum of all the forces is zero, and the object remains at rest or moves with constant velocity. Equilibrium is a crucial concept in statics, where it's used to analyze structures and systems at rest.
In summary, the net force formula is a fundamental concept in physics that describes how multiple forces acting on an object combine to produce a single resultant force. It is a vector quantity, considering both magnitude and direction. The net force is calculated by summing the individual forces, and it plays a central role in understanding the motion and behavior of objects in various fields of science and engineering. Newton's Second Law relates the net force, mass, and acceleration, providing a fundamental link between forces and motion. Free-body diagrams and the concept of equilibrium are useful tools in analyzing complex force situations. Understanding the net force is essential for solving a wide range of physics and engineering problems.
