

The concept of resultant force Formula is fundamental in physics and engineering, as it helps us understand how multiple forces acting on an object combine to produce a single net force. This net force determines the object's motion, and a comprehensive understanding of the resultant force is crucial in various applications, from designing structures to analyzing the motion of objects. In this essay, we will delve into the details of the resultant force, its definition, calculation, and significance in different contexts.
Definition Of Resultant Force
Resultant force, often referred to as the net force, is a vector quantity that represents the overall effect of multiple forces acting on an object. Forces are typically represented as vectors because they have both magnitude and direction. When multiple forces act on an object, the resultant force is the single force that can replace all these forces without altering the object's motion. In other words, it is the vector sum of all the individual forces.Also Check - Thermodynamics Formula
Mathematically, the resultant force F can be defined as: F= ⅀ F i Where: - F_is the resultant force vector. - ⅀ represents the summation symbol. - Fi represents each individual force vector acting on the object. To calculate the resultant force accurately, we need to consider both the magnitudes and directions of the individual forces.Also Check - Surface Tension Formula
Vector Addition Vector addition is the process of combining vectors to find their resultant. When dealing with forces, vector addition involves considering the magnitude and direction of each force. There are two main methods for vector addition: graphical methods and trigonometric methods.Graphical Method:
The graphical method involves drawing the vectors to scale on a piece of paper and then using geometric techniques to find the resultant vector. Here are the steps: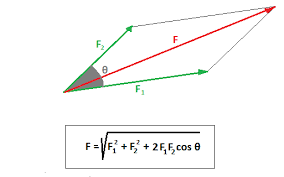
- Draw each force vector on a piece of paper, making sure to represent both magnitude and direction.
- Place the vectors' tails (starting points) at the same point (the origin).
- Connect the head (end point) of the last vector to the origin. This line represents the resultant force vector.
- Measure the length of the resultant vector and the angle it makes with a reference axis (usually the positive x-axis).
- Use trigonometric functions (sine, cosine, and tangent) to find the components of the resultant force along the x-axis and y-axis.
- Express the resultant force vector in terms of its magnitude and direction, often using polar coordinates (magnitude and angle).
Also Check - Rotation Motion Formula
Trigonometric Method:
The trigonometric method involves using trigonometric functions to calculate the resultant force's components along different axes. Here are the steps:- Break down each force vector into its x and y components. This is done using trigonometric functions:
Where:
- F_ix) is the x-component of the ith force. - F_iy) is the y-component of the ith force. - F_i) is the magnitude of the ith force. - (theta_i) is the angle of the ith force with respect to a chosen reference axis (usually the positive x-axis).- Sum all the x-components to find the total x-component of the resultant force and sum all the y-components to find the total y-component:
- Calculate the magnitude of the resultant force using the Pythagorean theorem:
- Express the resultant force vector in terms of its magnitude and direction (polar coordinates).
Also Check - Properties of Matter Formula
Applications of Resultant Force
To illustrate the practical applications of the resultant force, let's consider a few examples:- Statics: When analyzing a structure like a truss or a bridge, engineers use the concept of resultant force to determine whether the structure is in equilibrium or if it is subjected to an unbalanced force, which could lead to failure.
- Forces in Flight: In aviation, the resultant force of thrust, drag, lift, and weight determines an aircraft's motion. Engineers need to calculate and control these forces to ensure safe and efficient flight.
- Tension in Cables: When lifting heavy objects with cables or ropes, the tension in the cables can be complex due to multiple forces. Calculating the resultant force in the cables helps ensure safe lifting operations.
- Projectile Motion: When studying the motion of projectiles, such as a thrown baseball or a launched missile, understanding the resultant force is essential to predict the trajectory and landing point accurately.
- Sailing: Sailboats use the resultant force of wind on their sails to propel themselves forward. Sailors adjust the angle of the sails to control the direction and speed of the boat.
- Vehicle Dynamics: In automotive engineering, the resultant force of engine power, friction, and aerodynamic drag affects a vehicle's acceleration and top speed. Engineers optimize these forces for performance and fuel efficiency.
Resultant Force Formula FAQs
What is the difference between resultant force and individual forces?
How do you find the resultant force when forces act at different angles?
Can the resultant force be zero even when multiple forces are acting on an object?
What are some real-world examples where understanding resultant forces is crucial?











