Rotational Motion Formula - Definition, Examples

Definition And Formula Of Rotational motion

What is Motion?

Types of Motion

• Rotational Motion: Rotational motion, also known as angular motion, involves the spinning or rotating movement of an object around a fixed axis. All points of the object move in circular paths around the axis of rotation.
• Circular Motion: A rotational motion known as circular motion involves an object rotating in a circle around a central point. It can be uniform circular motion (constant speed along the circular path) or non-uniform circular motion (changing speed along the circular path).
• Oscillatory Motion: Oscillatory motion is repetitive back-and-forth movement around an equilibrium position. It is characterised by periodic motion, where an object moves between two points in opposite directions.

Also Check - Simple Harmonic Motion Formula

What is Rotational Motion?

Also Check - Thermodynamics Formula

Formulas of Rotatory Motion

• Angular Displacement ( ):

• Angular Velocity ( ):

• Tangential Velocity ( v ):

Download PDF Rotational Formula

• Angular Acceleration ( a ):

• Centripetal Acceleration ( ac ):

• Moment of Inertia (I):

• Torque (τ):

• Angular Momentum (L):

• Rotational Kinetic Energy ( K rot ):

Also Check - Work, Energy & Power Formula

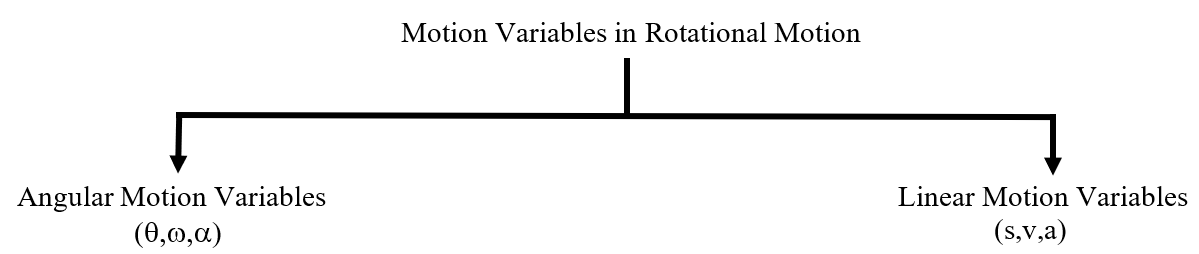
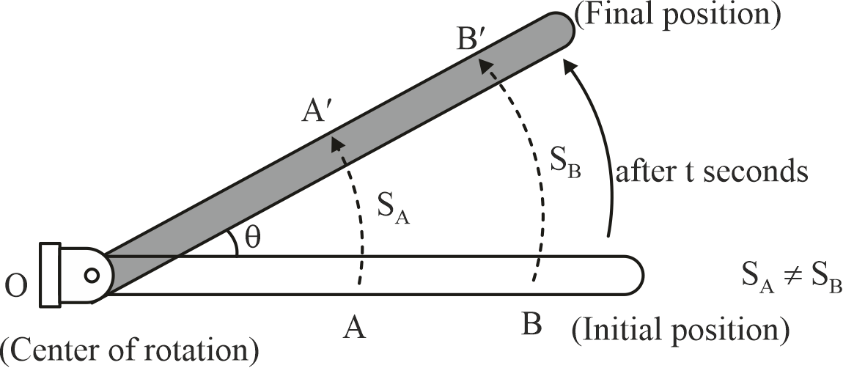
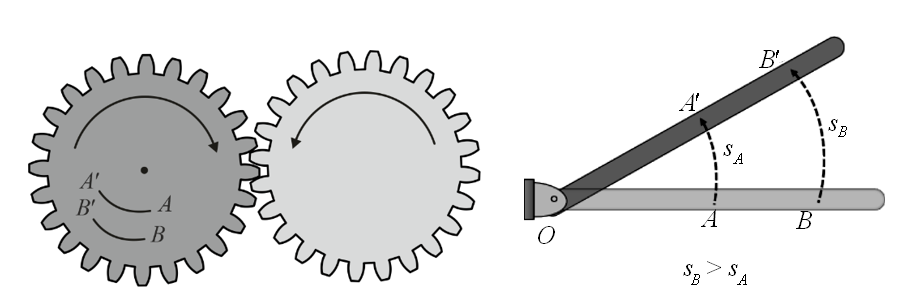
Properties of Rotational Motion

• Axis of Rotation: The rotation axis is a fixed point or line that all points on a spinning object follow in circular motions. The axis can be internal or external to the object, depending on the type of motion.
• Tangential Velocity: At any given point on the rotating object, the tangential velocity is the instantaneous linear velocity tangent to the circular path. It represents the speed at which that specific point is moving along its circular trajectory.
• Angular Displacement: Angular displacement measures the change in the angle of an object as it rotates from one position to another. It is usually represented by the symbol θ and is measured in radians or degrees.
• Angular Velocity: Angular velocity is defined as the rate at which an angular displacement changes over time. It represents how fast an object is rotating and is denoted by the symbol ω. Angular velocity is a vector quantity and points along the axis of rotation.
• Angular Acceleration: Angular acceleration is a unit of measurement for the rate of change in angular velocity with respect to time. It indicates how quickly the rotational speed of the object is changing and is represented by the symbol α.
• Moment of Inertia: The moment of inertia (also known as rotational inertia) quantifies an object's resistance to changes in its rotational motion. It is determined by the object's mass distribution as well as the axis of rotation.
• Torque: Force's rotational counterpart is torque. It results in a shift in angular momentum, which creates rotational motion. The product of the force applied and the perpendicular distance from the axis of rotation to the site of application of the force determines the torque operating on an item.
• Conservation of Angular Momentum: Like linear momentum, angular momentum is conserved in an isolated system when no external torques act upon it. This conservation principle plays a crucial role in understanding many rotational phenomena.
• Centripetal Force: In circular motion, there is a centripetal force acting towards the center of the circular path, responsible for keeping the object in that trajectory. For rotational motion, this force is essential for maintaining the circular path of each point on the object.
• Gyroscopic Stability: Gyroscopic stability is a unique property of rotating objects, like gyroscopes. It allows them to maintain their orientation and resist changes in their rotational axis, even when external forces act upon them.
• Rotational Kinetic Energy: The kinetic energy associated with an object's rotation is known as rotational kinetic energy. It is determined by the moment of inertia and angular velocity of the object.