RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 (Ex 3C) Squares and Square Roots
Neha Tanna31 Jul, 2024
Share
RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3: The Physics Wallah academic team has provided a comprehensive answer for Chapter 3: Squares and Square Roots in the RS Aggarwal class 8 textbook. The RS Aggarwal class 8 solution for Chapter 3 Squares and Square Roots Exercise-3C is uploaded for reference only; do not copy the solutions.
Before going through the solution of chapter-3 Squares and Square Roots Exercise-3C, one must have a clear understanding of Chapter 3 Squares and Square Roots. Read the theory of Chapter 3 Squares and Square Roots and then try to solve all numerical of exercise-3C. For class 8 maths students, the NCERT textbook is a highly recommended resource for solving numerical problems and referencing NCERT solutions.RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 Squares and Square Roots Overview
Chapter 3 of RS Aggarwal's Class 8 Maths textbook, focused on Squares and Square Roots, continues with Exercise 3.3, which deepens students' understanding of these fundamental concepts. This exercise presents a variety of problems aimed at reinforcing the calculation of square roots, particularly emphasizing the use of the long division method for finding square roots of non-perfect squares. In Exercise 3.3, students encounter problems that require them to apply their knowledge of prime factorization and long division methods to determine square roots. The problems are designed to challenge students and enhance their computational accuracy and problem-solving skills. The exercise also includes real-world applications, helping students see the relevance of these mathematical concepts in everyday life. Through a structured approach, this exercise helps students develop a systematic method for finding square roots, an essential skill in higher mathematics. It also encourages logical thinking and precision, as students must carefully follow steps to arrive at the correct answer.RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 (Ex 3c)
The two ideas are diametrically opposed to one another. The numbers that result from multiplying a value by itself are called squares. In contrast, a number's square root is a value that, when multiplied by itself, returns the original value. Both are hence vice-versa techniques. For instance, two squares equal four, and two square roots equal four. If n is a number, then its square root is written as "√n," where "√" is referred to as radical, and its square is represented by n raised to the power 2, or n2. Radicand refers to the value that appears underneath the root symbol. The area of a square form is frequently used to explain square numbers. An equal number of sides make up the shape of a square. Consequently, side x side or side2 equals the area of a square. Therefore, the square's size is 32 = 9 sq. cm if its side length is 3 cm.RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 PDF
Below we have provided RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 Squares and Square Roots in detail. This chapter will help you to clear all your doubts regarding the chapter. Students are advised to prepare from these RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 before the examinations to perform better.RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 PDF
RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3
Below we have provided RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 Squares and Square Roots –Find the value of the following, using the column method:
(1) (23) 2
Solution: Given number 23 = 20 + 3 Here, a = 20 and b = 3| a 2 | 2ab | b 2 |
| (20) 2 = 400 | 2 × 20 × 3 = 120 | (3) 2 = 9 |
(2) (35) 2
Solution: Given number 35 = 30 + 5 Here, a = 30 and b = 5| a 2 | 2ab | b 2 |
| (30) 2 = 900 | 2 × 30 × 5 = 300 | (5) 2 = 25 |
(3) (52) 2
Solution: Given number 52 = 50 + 2 Here, a = 50 and b = 2| a 2 | 2ab | b 2 |
| (50) 2 = 2500 | 2 × 50 × 2 = 200 | (2) 2 = 4 |
| a 2 | 2ab | b 2 |
| (90) 2 = 8100 | 2 × 90 × 6 = 1080 | (6) 2 = 36 |
Find the value of each of the following, using the diagonal method:
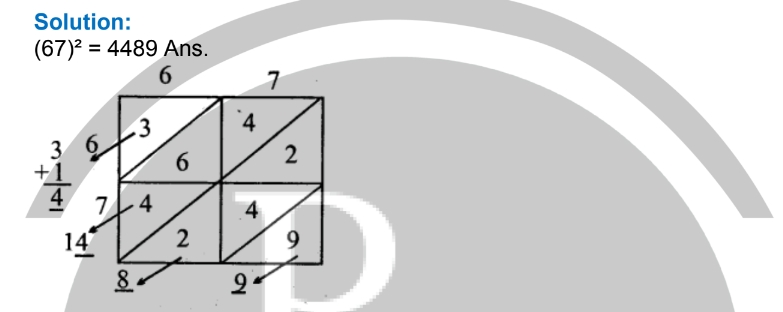
(5) (67) 2
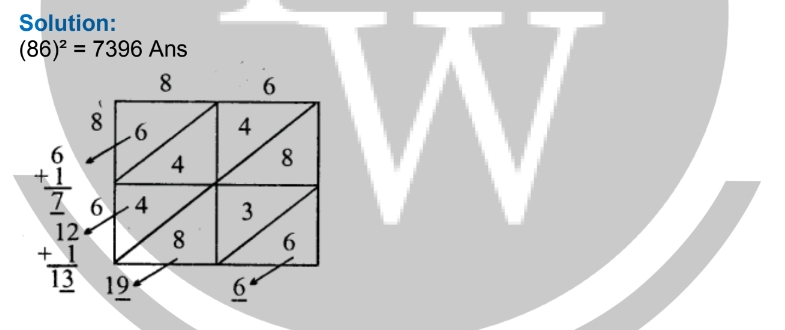
(6) (86) 2
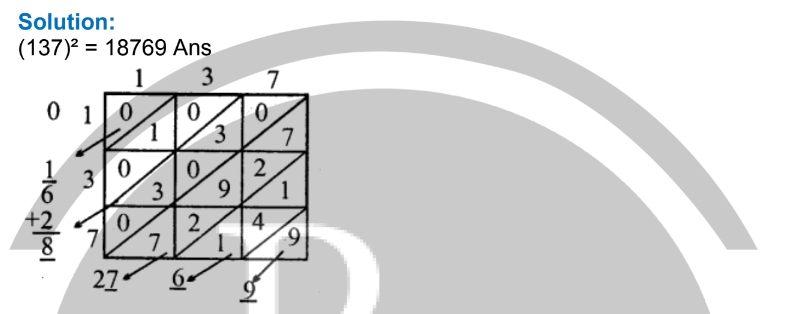
(7) (137) 2
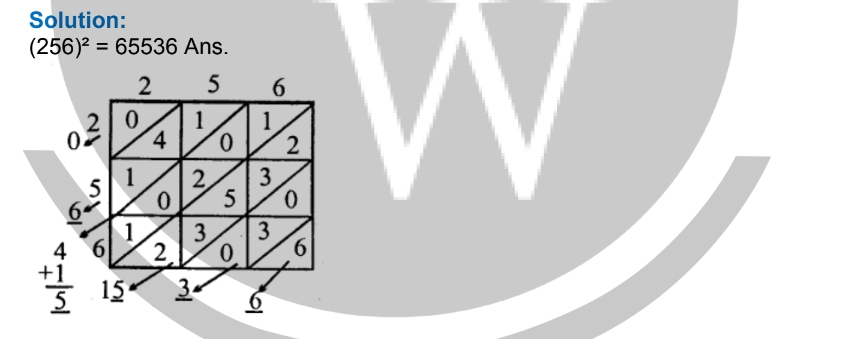
(8) (256) 2
Benefits of RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3
The RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 on Squares and Square Roots offer numerous benefits to students, enhancing their understanding and proficiency in this essential mathematical topic:Comprehensive Understanding : The solutions provide clear, step-by-step explanations of each problem, helping students grasp the underlying concepts of squares and square roots more thoroughly.
Skill Development : By practicing with these solutions, students develop key skills such as prime factorization and the long division method for finding square roots. This practice is essential for mastering more complex mathematical problems.
Enhanced Accuracy : The detailed solutions help students improve their calculation accuracy. Regular practice ensures they can perform these operations correctly and confidently.
Effective Exam Preparation : The solutions are aligned with the curriculum and exam patterns, making them an excellent resource for exam preparation. Students can use them to review and practice, ensuring they are well-prepared for assessments.
Error Analysis and Correction : Comparing their work with the provided solutions allows students to identify and understand their mistakes. This process of error analysis helps them learn and avoid similar mistakes in the future.
Confidence Building : Regular practice with guided solutions boosts students' confidence. As they become more familiar with the methods and concepts, their overall confidence in handling mathematical problems increases.
RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 FAQs
What are the square numbers for Class 8?
What is square formula 8 class?
What is square and square roots for beginners?
Is RS Aggarwal Solutions for Class 8 Maths Chapter 3 Exercise 3.3 Squares and Square Roots helpful?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
