Trusses are widely used in civil and mechanical engineering to construct lightweight and sturdy structures. The analysis of trusses is essential to determine the internal forces in each member, which helps in designing efficient and safe structures. The two main analytical methods for truss analysis are: method of joints and method of section. These methods offer alternative approaches to calculate internal forces in truss members and provide valuable insights into the behavior of complex truss systems.
Assumptions in the Analysis of Plane Truss
The following key assumptions are made for truss analysis:
-
All truss members are idealized as straight elements, and they are connected only at their ends, meaning each member behaves as a straight two-force member.
-
All joints are frictionless pin joints.
-
Loads (external forces) are only applied at the joints.
-
The weight of the members is assumed negligible.
Note:
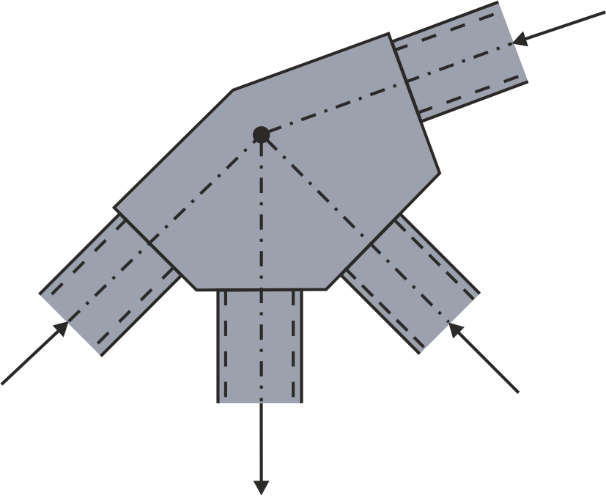
When structural members are connected using welded or riveted joints, it is generally acceptable to assume that the connection acts as a pin joint if the centerlines of the members intersect at the joint, as shown in the figure below:
Method of Section
The Method of Sections, also known as Ritter's method, is a powerful approach used to analyze truss structures by considering equilibrium of a section. This technique involves strategically cutting the truss by one or more sections that pass through the specific members in which the internal forces need to be determined. By carefully considering the equilibrium of one part of the cut truss, we can efficiently determine the unknown forces in those members.
This method proves to be particularly advantageous over the method of joints when we only need to calculate forces in a select few truss members, as it saves significant time and effort compared to analyzing the entire structure. The simplicity and selectivity of the Method of Sections make it an invaluable tool in truss analysis. The subsequent steps outline the Method of section for truss analysis.
Step 1:
Calculate support reactions by considering the equilibrium of the entire truss structure, if needed.
Note: Not all the reactions need to be calculated, rather calculate only those, which are included in the selected cut part for further analysis.
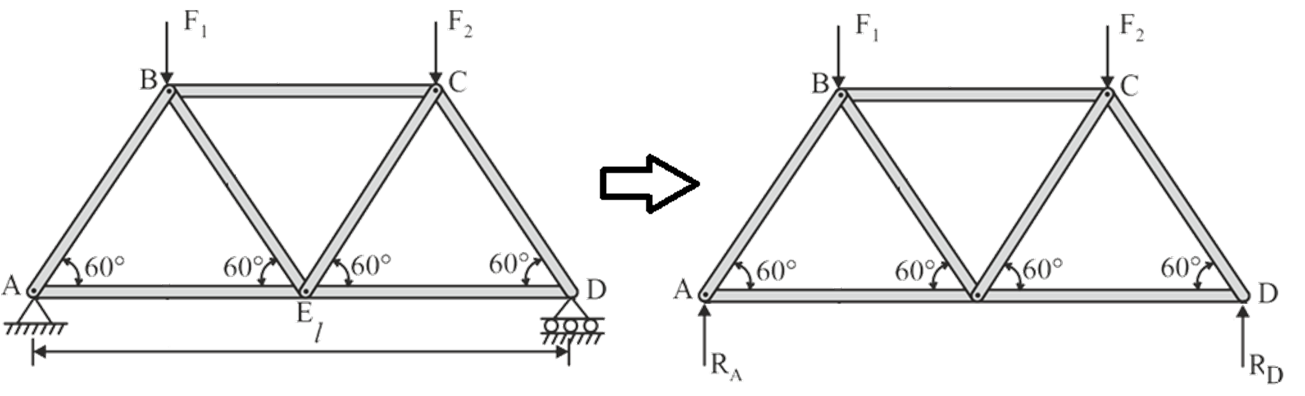
Step 2:
Divide the truss using a section line, which can be straight or curved, into two parts while ensuring that it preferably intersects no more than three unknown members.
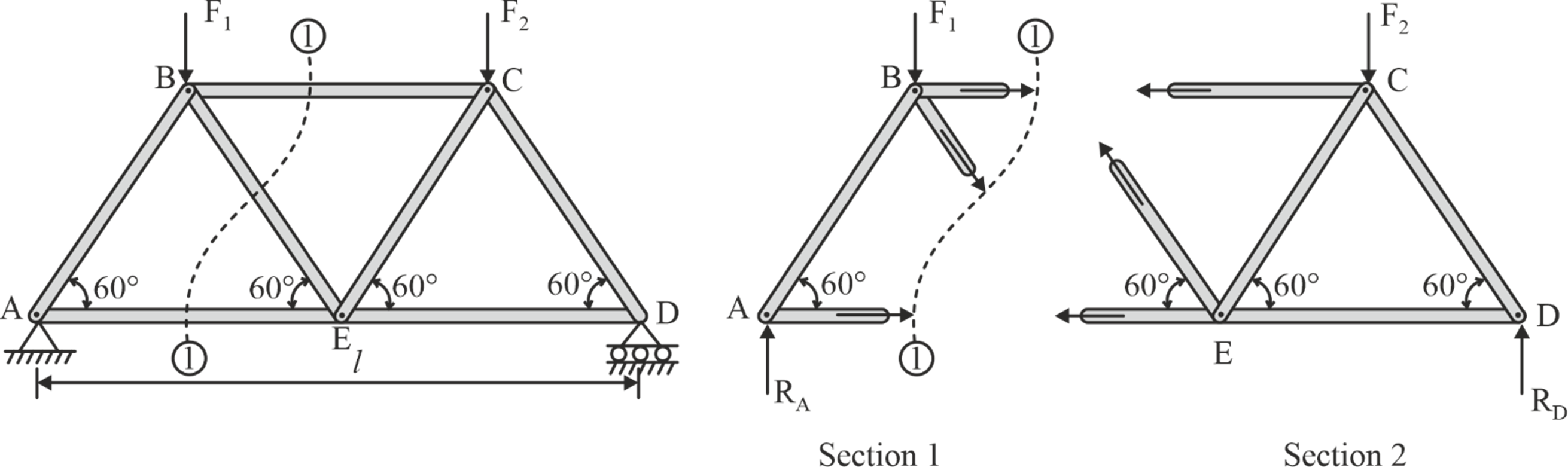
Step 3:
Choose an appropriate section of the truss and create its Free Body Diagram (FBD), encompassing all internal and external forces acting on the selected portion (As shown above). Assume tension or compression in the cut members.
Step 4:
Consider the equilibrium of the section and apply the equations of equilibrium,(ΣF
x
= 0 , ΣF
y
= 0 and ΣM = 0 ) to calculate the unknown forces.
Note:
-
Preferably, use ΣM = 0 by selecting a suitable point for moment calculation where two known forces pass through. It's important to note that the point for moment calculation may or may not coincide with the Free Body Diagram (FBD) of the truss.
-
Usually, we limit the cut members to three, as we have three equations of equilibrium to find three unknowns. Yet, in exceptional cases where many members are collinear or concurrent, we can cut more than three members. By selecting an appropriate moment center where the line of action of all but one cut member passes, we can determine the required unknown forces.
Example Problem
Calculation of force in member BD in given plane truss.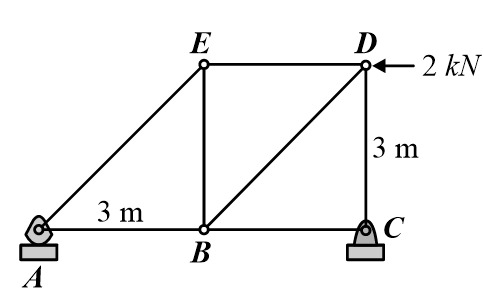
Solution:
Calculation of reaction at support A;
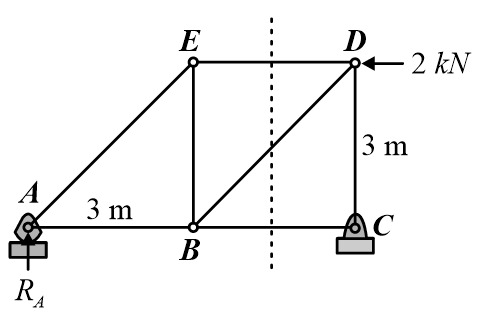
ΣM
C
= 0
R
A
× 6 = 2 × 3
R
A
= 1 kN
Cut the truss by a section line (as shown above) passing through members ED, BD and BC and consider the equilibrium of the any side section of the truss for analysis of unknowns. In this problem equilibrium of the left side section is considered ;
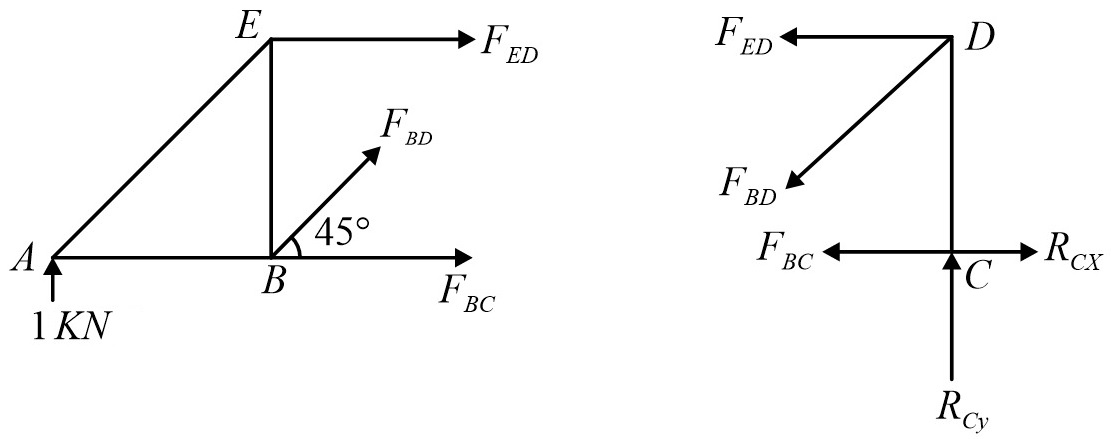
ΣFy = 0
F
BD
sin 45° + 1 = 0
F
BD
= –1. 414 kN
F
BD
=
1. 414 kN, Compression
