
Collision of Bodies: In the realm of engineering mechanics, the study of collisions holds immense importance in understanding the behavior and interactions of bodies in motion. Whether it's analysing the impact of vehicles in accidents, predicting the effects of machinery collisions, or assessing the resilience of structures against impacts, a comprehensive understanding of collision mechanics is essential for engineers.
A collision can be defined as “ an event that occurs when two or more bodies interact by physically coming into contact for a very short period of time and exert very large force on each other, resulting in the exchange of energy and/or momentum between them ”. During collisions, energy and momentum exchange, resulting in a change in the objects' velocities and trajectories. In physics, collision is also referred to as "impact."
In our daily lives, we often observe collisions between bodies. Examples include the collision between a leg and a football, the collision between two coins in carrom, the collision between a bat and a ball, and the collision between a dropped object and the floor. These instances highlight the dynamic exchange of energy and momentum that occurs during each collision.
Type of Collision of Bodies
Collision of bodies can be classified based on the direction of motion of colliding bodies relative to the line of impact. Here is the classification:
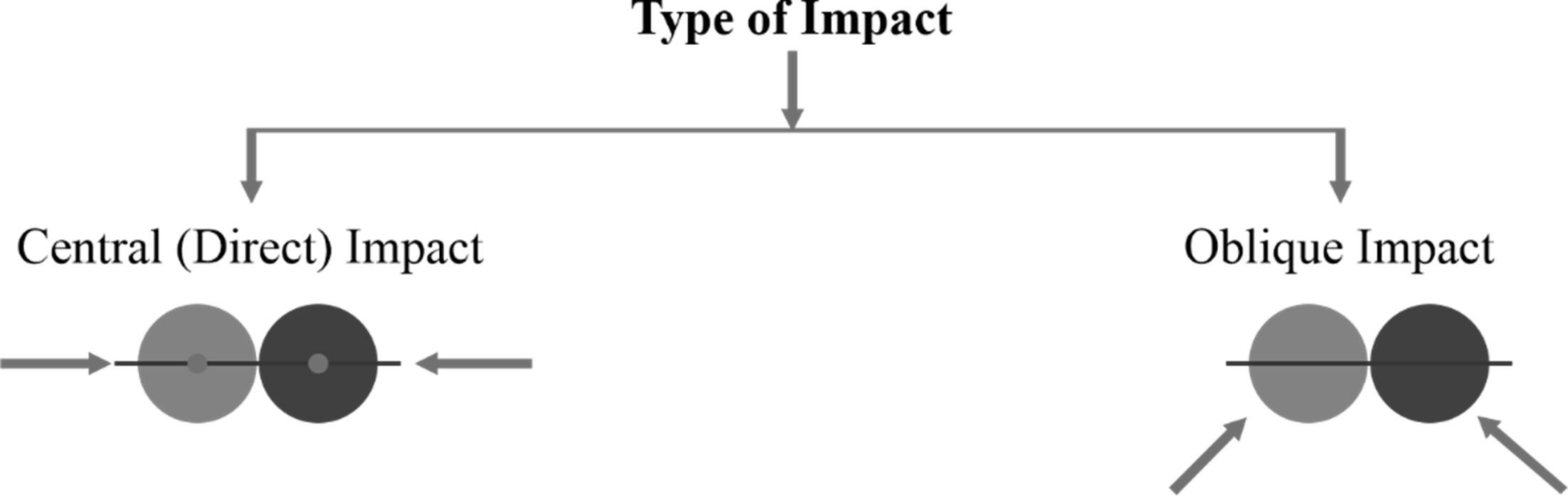
Central (Direct) Impact
In a direct collision, two bodies collide head-on along the same line of motion. In other words, “collision occurs with the contact forces directed along the line of centers.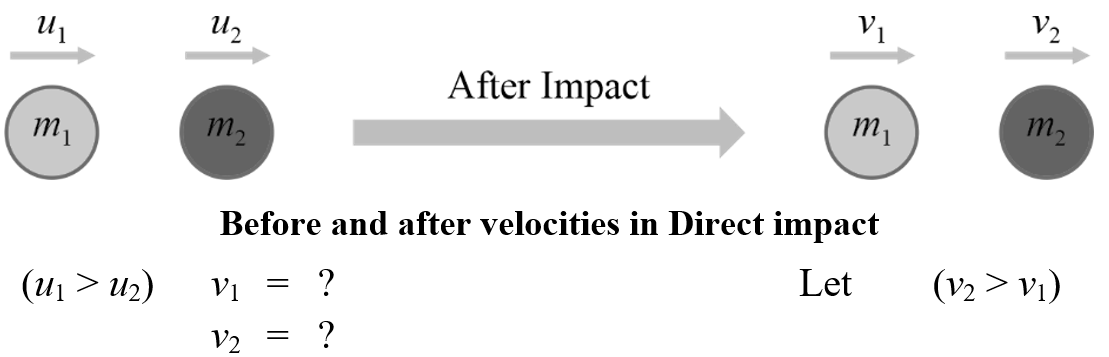
Oblique Impact
Oblique collision refers to a collision between two bodies in which the velocities of approach are at an angle other than directly head-on. In an oblique impact, the bodies collide along a line of impact that is not parallel or perpendicular to their initial velocities.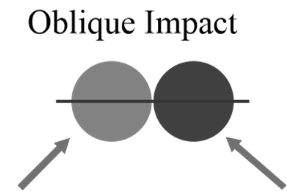 Collision of bodies can also be classified
based on the elasticity of the bodies involved
. Elasticity refers to the ability of a body to undergo deformation when subjected to an external force and then return to its original shape and size after the force is removed. Here are the classifications of collisions based on elasticity;
Collision of bodies can also be classified
based on the elasticity of the bodies involved
. Elasticity refers to the ability of a body to undergo deformation when subjected to an external force and then return to its original shape and size after the force is removed. Here are the classifications of collisions based on elasticity;
1. Perfectly Elastic Collision
A perfectly elastic collision is a collision where the bodies bounce off each other without any loss of kinetic energy. Perfectly elastic collisions are idealized and not typically observed in real-world scenarios. In perfectly elastic collisions;- Momentum is conserved.
- Kinetic energy is conserved.
2. Inelastic Collisions
In an inelastic collision, the colliding bodies deform upon impact and may stick together or experience a loss of kinetic energy. In these collisions, momentum is conserved, but kinetic energy is not fully conserved. Inelastic collisions can be further classified into two categories: perfectly inelastic collision and partially inelastic collision.(i) Perfectly Inelastic Collision
A perfectly inelastic collision is a type of inelastic collision where the colliding bodies stick together and the bodies move as a single entity with a common final velocity after the impact. Maximum deformation occurs, and the kinetic energy is at its minimum. In perfectly inelastic collisions;- Momentum is conserved.
- Kinetic energy is not conserved.
(ii) Partially Inelastic Collision
In a partially inelastic collision, the colliding bodies may stick together for a brief period but eventually separate. Some kinetic energy is lost, and the bodies experience deformation. In partially inelastic collisions;- Momentum is conserved.
- Kinetic energy is not conserved.
Laws used in Collision of Bodies
Principle of Conservation of Momentum
The law of conservation of momentum states that “the total momentum of an isolated system remains constant before and after a collision, as long as no external forces are present”.Initial momentum of system = Final momentum of system
m 1 u 1 + m 2 u 2 = m 1 v 1 + m 2 v 2
Note: Assign the correct sign to the velocity values in the formula above, by designating one direction as positive
Newton’s Law of Restitution
For a given pair of bodies in collision, the ratio of relative velocity after collision and relative velocity before collision is always same.
- This ratio is known as coefficient of restitution ( e ). Its value depends on the material and it is the measure of the elasticity of a collision. Value of e lies in between zero and 1.
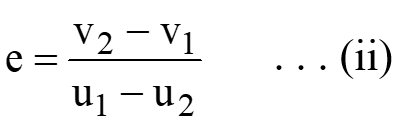
- The coefficient of restitution helps determine the degree of energy loss or preservation during a collision, aiding in the selection of materials, designing impact-absorbing structures, and optimizing machinery performance.
e = greater than zero and less than one for inelastic collision (0 < e <1)
e = 1 for perfectly elastic collision
e = 0 for perfectly plastic collision
Principle of Conservation of Kinetic Energy
The law of conservation of kinetic energy states that “the total kinetic energy of a system remains constant before and after the collision.- For perfectly elastic collision, kinetic energy of the system is conserved.
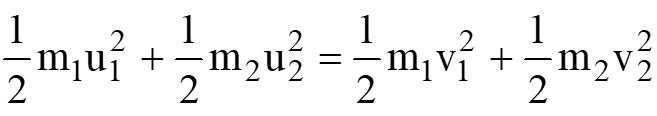
- If e < 1, some kinetic energy is lost.
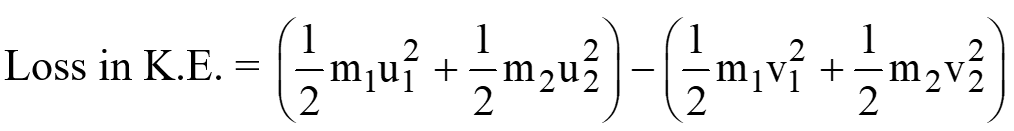
Special Case: Case 1
If there is perfectly elastic collision between two bodies, of equal masses, the velocities of the bodies interchange after collision.
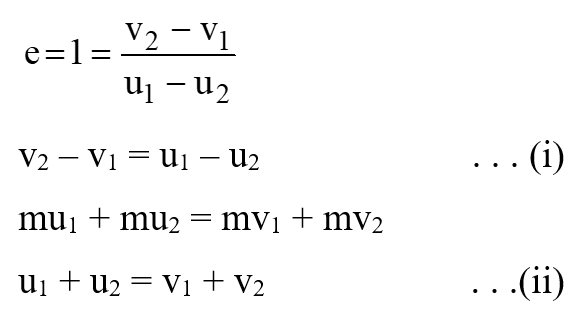
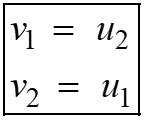
Special Case: Case 2
If there is perfectly plastic collision between two bodies, the bodies stick together and move as single body after collision.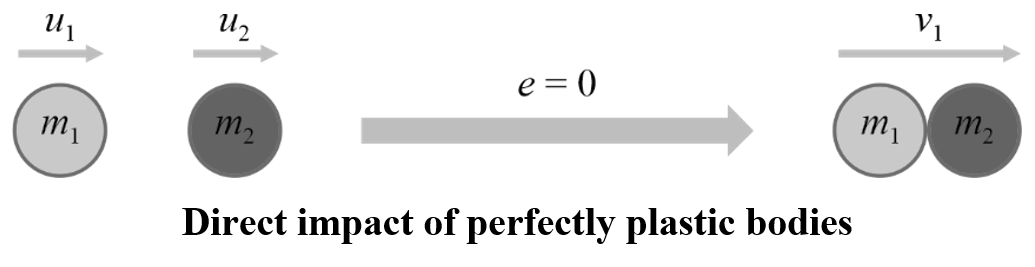
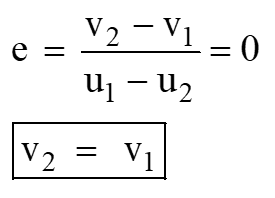
Some Practical Applications of Collision Studies in Engineering
- Vehicle Crash Safety: Understanding collision mechanics is vital in automotive engineering for designing vehicles with enhanced crash safety
- Structural Analysis and Design: In civil and structural engineering, collision analysis is crucial for assessing the resilience of structures against impacts such as earthquakes, explosions, or accidental collisions
- Machinery Safety and Reliability: Collision studies play a significant role in machinery design and safety. Engineers analyze collisions to prevent failures, minimize downtime, and optimize machine performance










