Introduction to Frames: In engineering mechanics, the study of structures is crucial as it forms the foundation for understanding how various mechanical components interact and support loads. Structures are an integral part of engineering systems, ranging from simple trusses to complex frames in bridges and buildings.
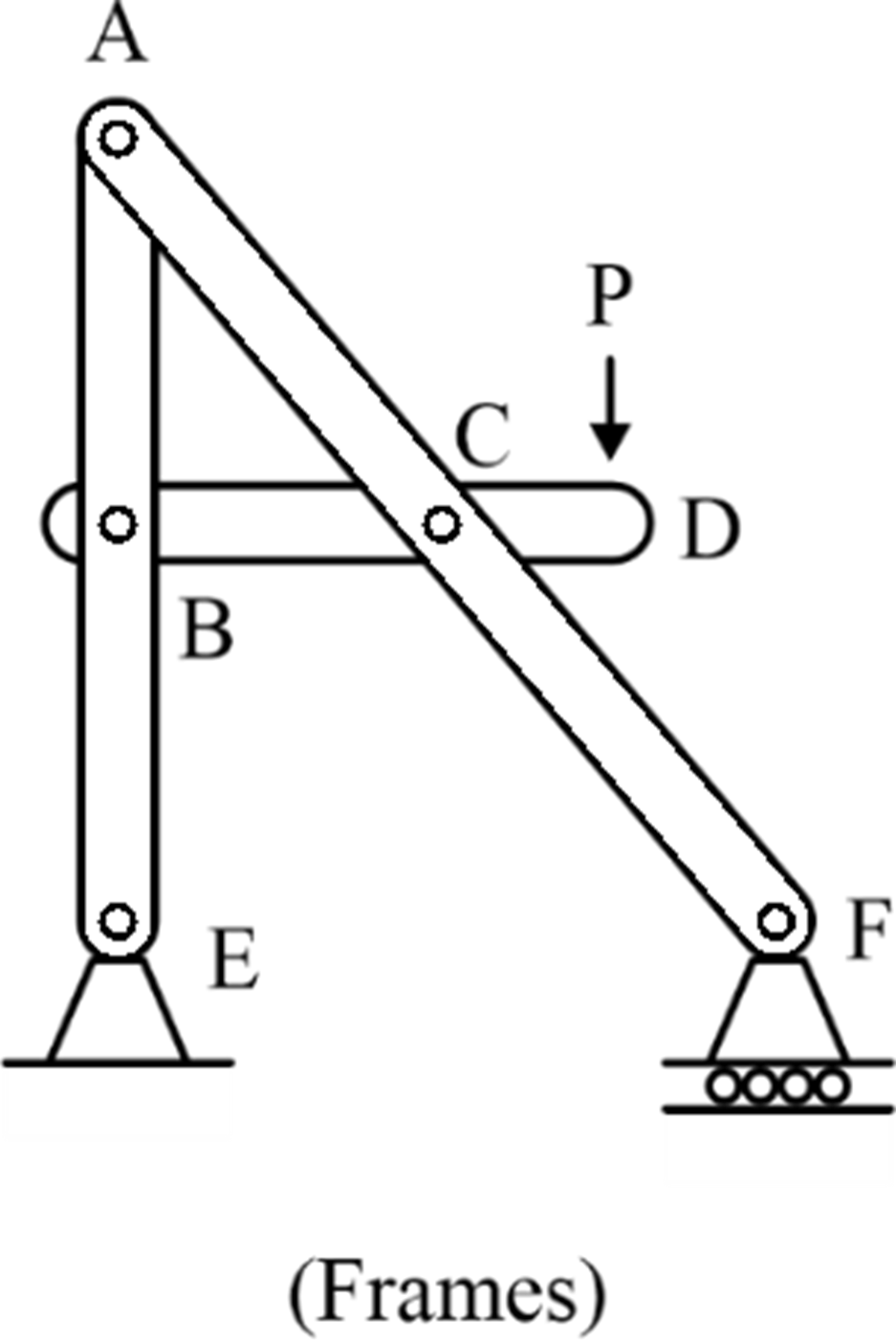
Frames are structures made of interconnected, inextensible members. Their purpose is to provide support for externally applied loads and moments. In simple words, " A structure that includes at least one multi-force member is termed as frame. Frames are essential components in various engineering applications, including buildings, bridges, and mechanical structures.
Multi-force Member
A multi-force member refers to a structural element that experiences, at three or more than three points, the influence of either two forces accompanied by a moment or a combination of more than two forces.
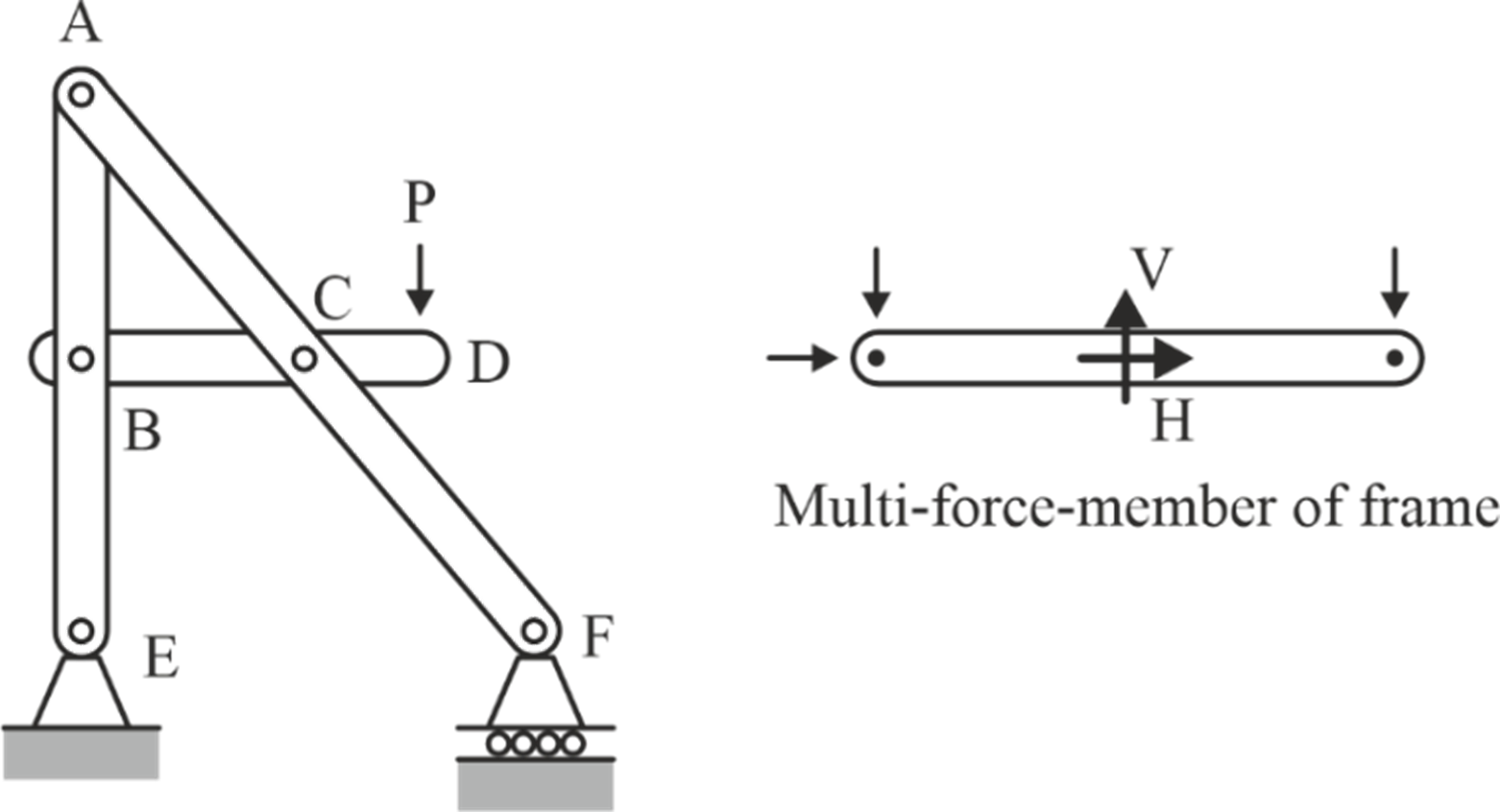
Note: Beam is always a multi-force member.
Truss vs Frames
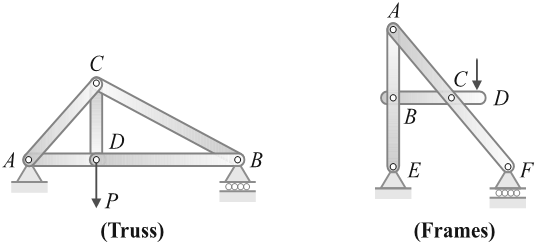
- Trusses exclusively experience forces along the members' axes, inducing either tension or compression. In contrast, frames encounter forces along the member axis as well as transverse forces, offering a more complex load scenario.
- Trusses have two-force members, while frames contain at least one multi-force member .
- In trusses, members are connected at the ends only, while in frame structures, the parts can be connected at the ends or also somewhere in the middle .
- In trusses, forces are concentrated at the joints, while frames can have forces distributed anywhere along their members .
- Frames do well at supporting complicated loads from multiple directions, making them suitable for multi-loaded constructions. Trusses are best suited for long spans such as bridges and roofs.
- Trusses consist of straight members, whereas frames can have a variety of member shapes and orientations.
Analysis of Plane Frames
Frames are analyzed by isolating their members and utilizing the equations of equilibriums (ΣF x =0, ΣF y =0, and ΣM=0) on the free body diagram of the isolated members.
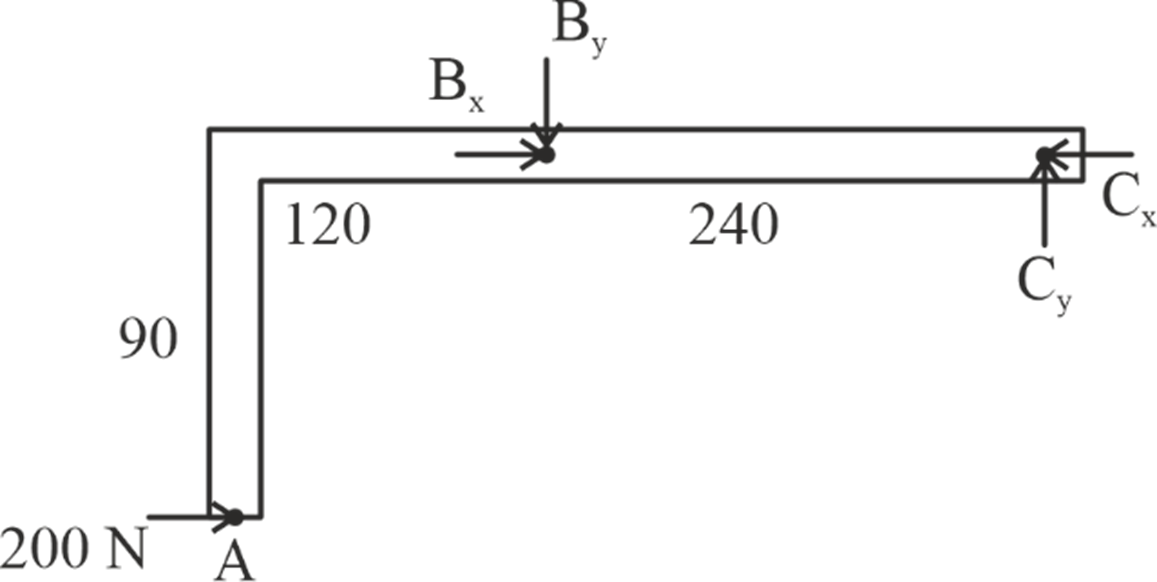
Example Problem
What is the magnitude of force at pin B?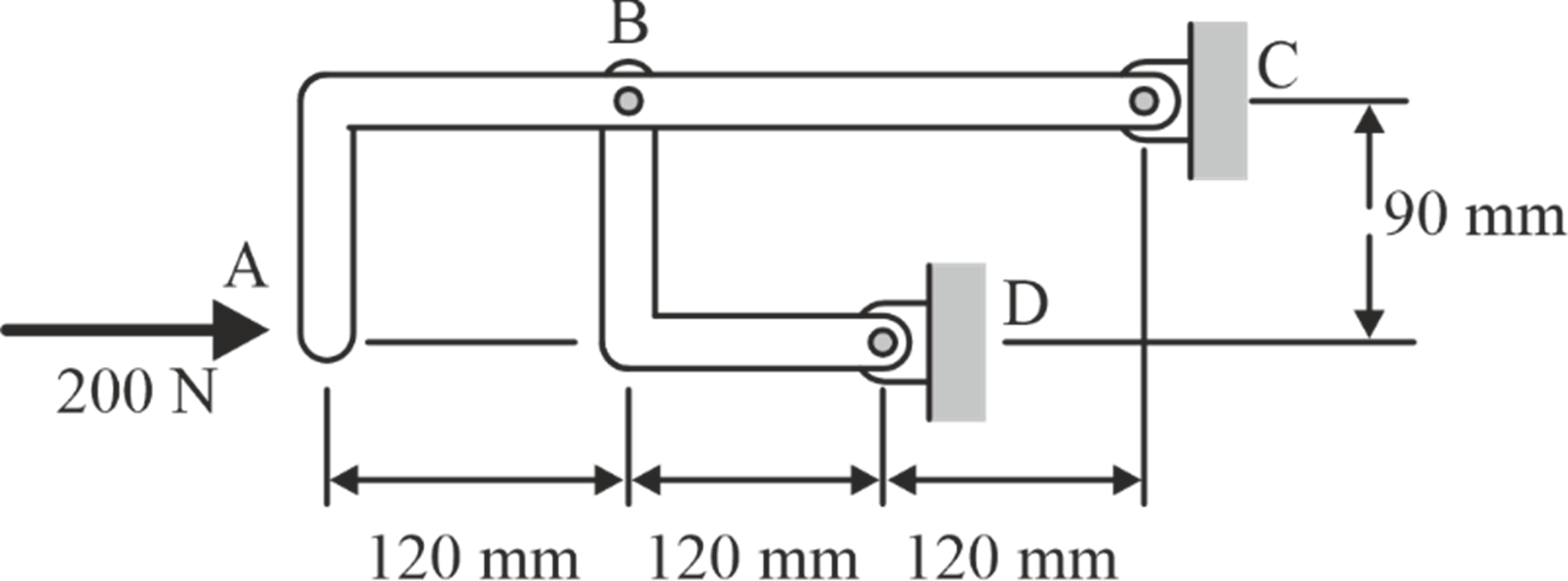
Solution:
Draw FBD of member BD
;
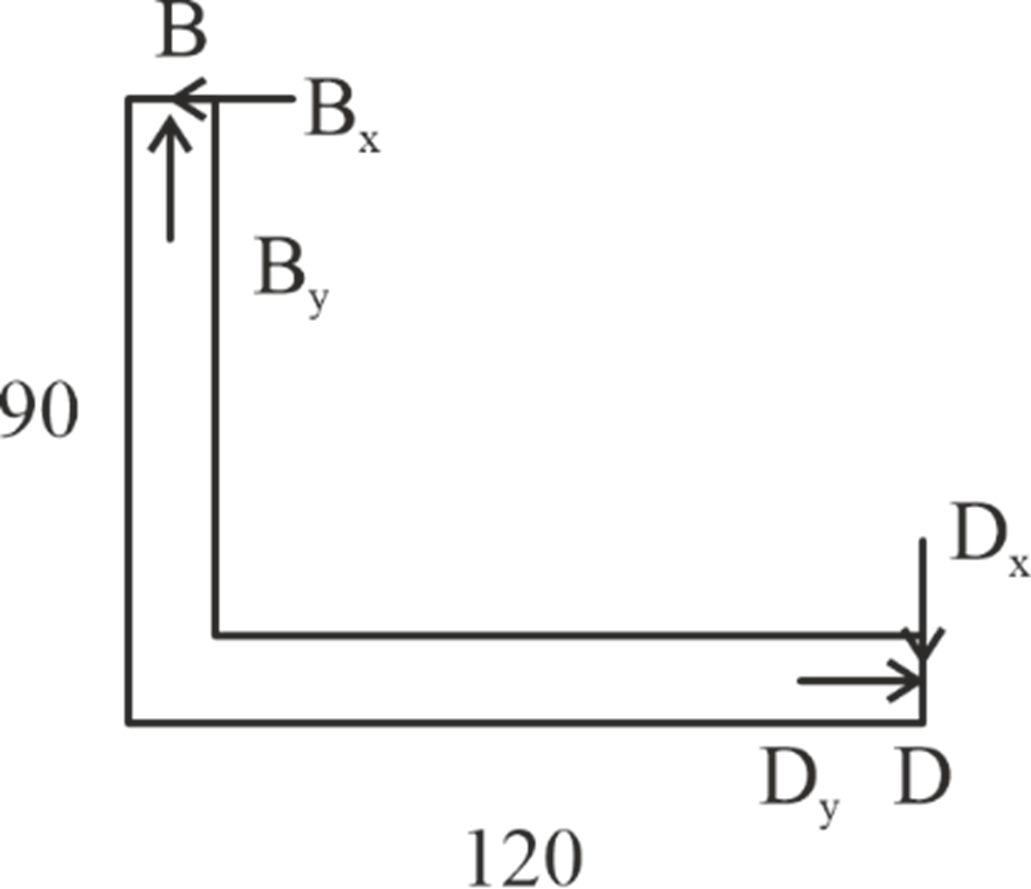
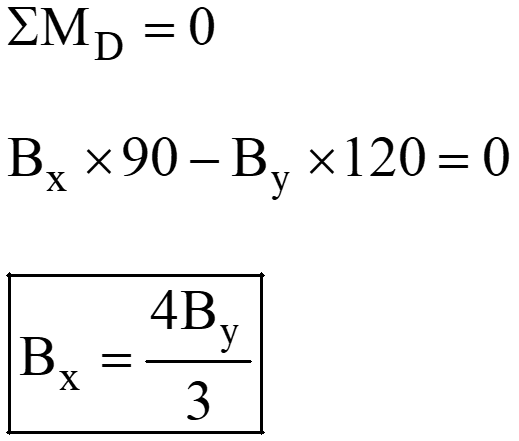
Draw FBD of member ABC;