Moment of Inertia and Radius of Gyration
Vikalp Tiwari7 Dec, 2023
Share
Moment of Inertia
The concept of moment of inertia is essential as it's a cornerstone in the analysis and design of mechanical systems, providing insight into the behavior of objects under the influence of torques. “Moment of Inertia" refers to a fundamental property of an object that quantifies its resistance to changes in rotational motion.
- Moment of inertia depends on the mass (or area) and its distribution from axis of rotation.
- The moment of inertia is a scalar quantity.
- Moment of Inertia can be classified into two main types:
Area Moment of inertia
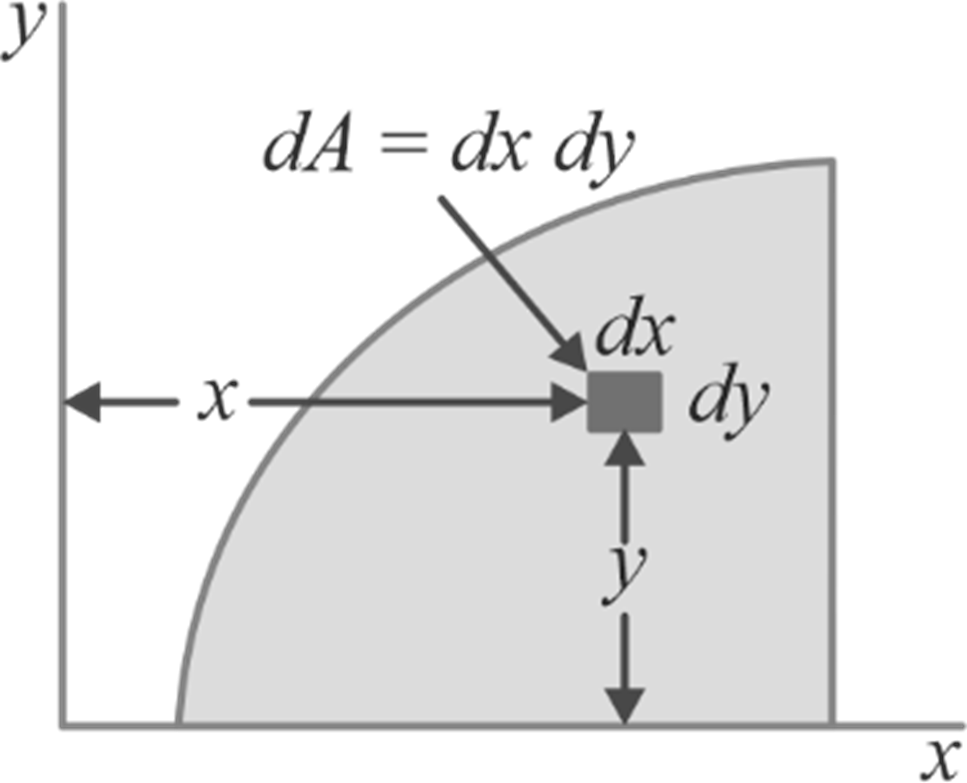
It signifies the resistance of an area against the applied moment (bending moment or twisting moment) about an axis. In simple words, " The second moment of area is the area moment of inertia ". Let's take into consideration a planar shape for which we need to determine the moment of inertia around both the x-x axis and the y-y axis, as shown in Figure. We'll divide the entire area into multiple smaller strips. Focus your attention on one of these individual strips.
Now, we can calculate the moment of inertia of the entire area about y-y axis by integrating the equation mentioned above, which is represented as:
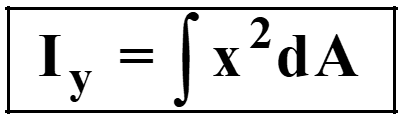Similarly, area moment of inertia of entire area about x-x axis;
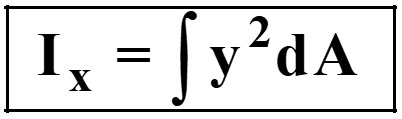
Polar Moment of Inertia
The moment of inertia of an area about the axis perpendicular to the plane of figure (i.e., normal axis or z axis) is known as polar moment of inertia.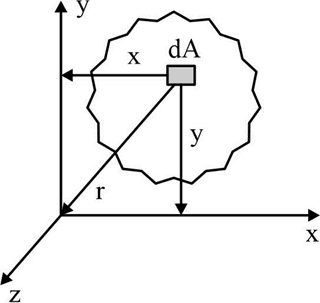
We can calculate the polar moment of inertia of the entire area by integrating the equation for the moment of inertia of the elemental area dA about the z-z axis.
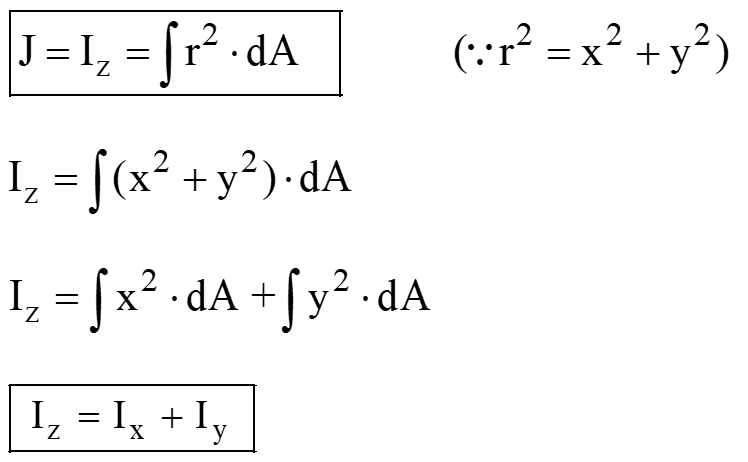
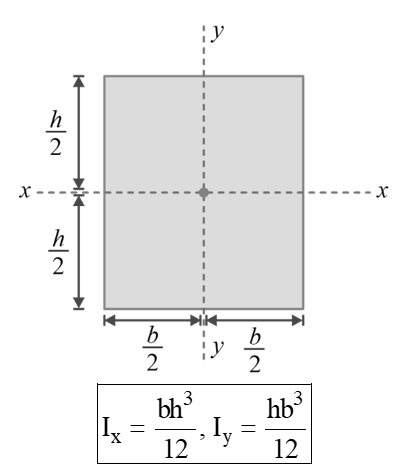
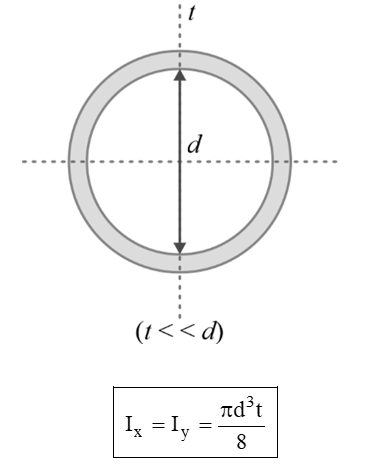
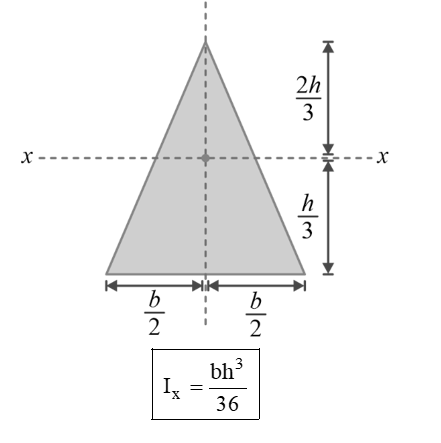
Area Moment of inertia of Some Common Areas
|
|
|
|
|
|
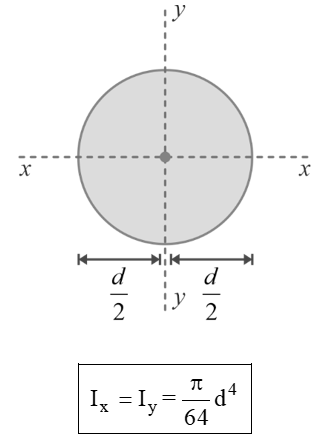
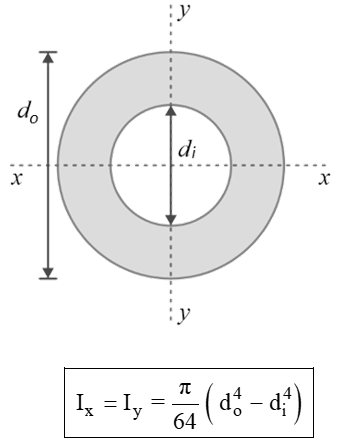
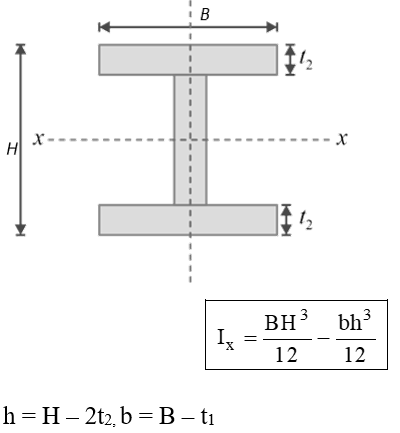
Mass Moment of Inertia
Mass moment of inertia is a crucial property that quantifies an object's resistance to rotational motion, similar to how mass characterizes resistance to translational motion. The Mass Moment of Inertia, often referred to as Rotational Inertia, constitutes the fundamental aspect of MOI. It specifically relates to how mass is distributed within an object. In simple words, “second moment of the mass is known as mass moment of inertia”.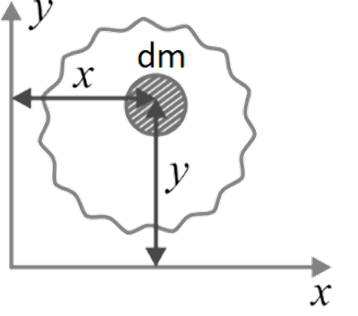
Mass moment of inertia of a body about x and y axis is given as;
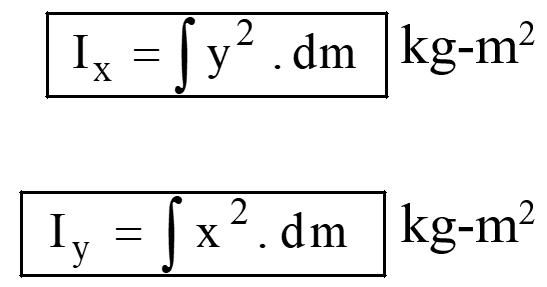
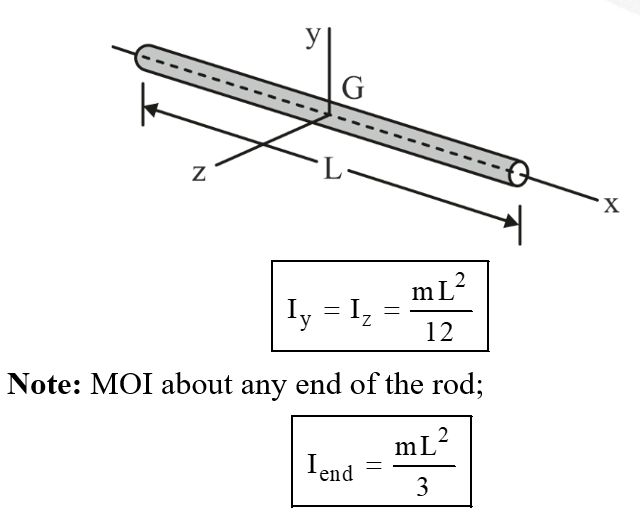
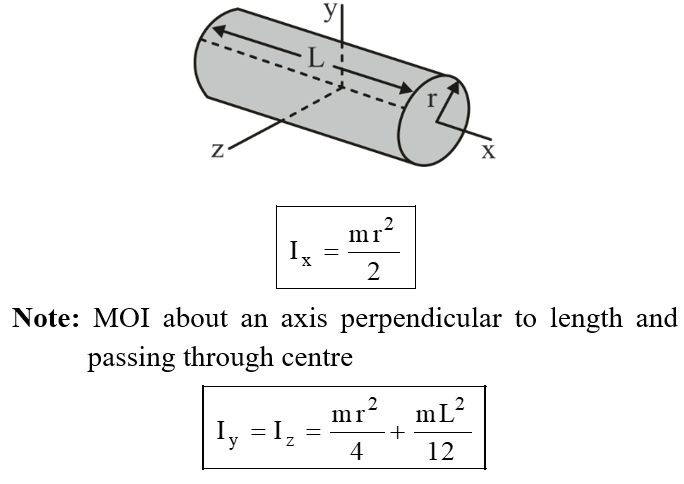
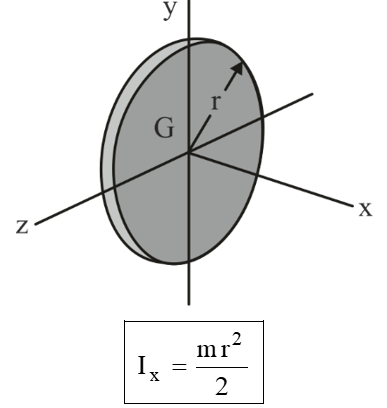
Mass Moment of inertia of Some Common Bodies
|
|
|
|
|
|
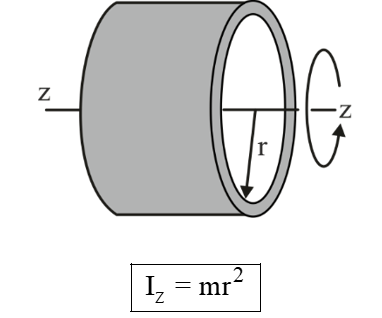
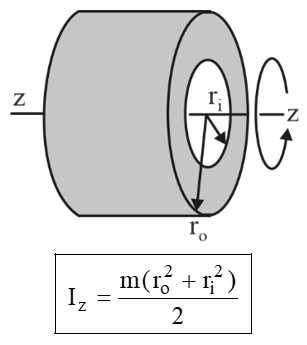
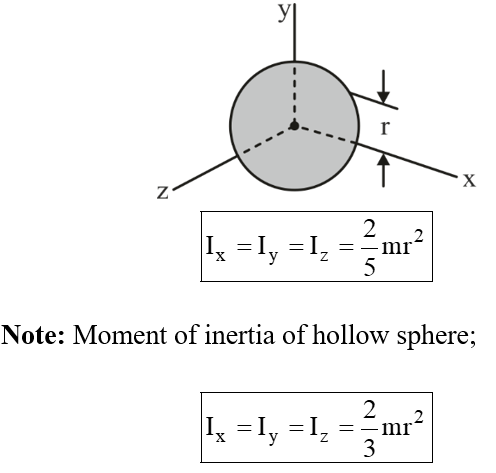
Radius of Gyration
The radius of gyration, also known as the gyradius, is a parameter used to characterize the distribution of mass (or area) within an object. It is the distance from a specified axis of rotation to a point where the entire mass (or area) of the object can be concentrated without altering its moment of inertia around that axis.
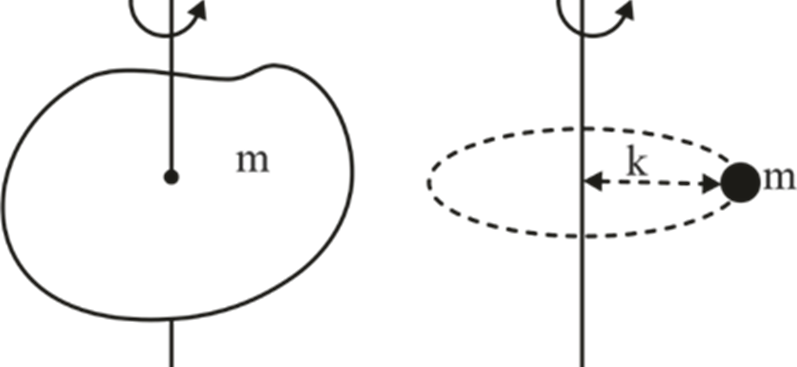If we can treat the entire mass(or area) of an object as if it were concentrated at a single point, creating the same resistance to rotation (or bending) as the actual mass (or area) distribution, then we can express the mass (or area) moment of inertia of the object as
The radius of gyration can be expressed as:
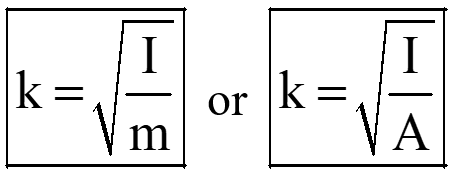
Moment of Inertia of Composite Areas/ Bodies
Follow these steps to determine the moment of inertia of a composite shape:
- Step 1: Divide the composite area into simpler known geometric areas.
- Step 2: Determine the moment of inertia for each basic geometric area about the desired axis, utilising the parallel axis theorem.
- Step 3: Algebraically sum the individual moments of inertia of the simpler areas to obtain the moment of inertia for the composite area.
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
