Motion a Car on a Banked Road :
When vehicles go through turnings, they travel along a nearly circular arc. There must be some force which will provide the required centripetal acceleration. If the vehicles travel in a horizontal circular path, this resultant force is also horizontal. The necessary centripetal force is being provided to the vehicles by following three ways:
1.
By friction only.
2.
By banking of roads only.
3.
By friction and banking of roads both.
In real life, the necessary centripetal force is provided by friction and banking of roads both. Now, let us write equations of motion in each of the three cases separately and see what the constraints in each case are. When vehicles go through turnings, they travel along a nearly circular arc. There must be some force which will produce the required acceleration. Friction is not always reliable at circular turns if high speeds and sharp turns are involved. To avoid dependence on friction, the roads are banked at the turn.
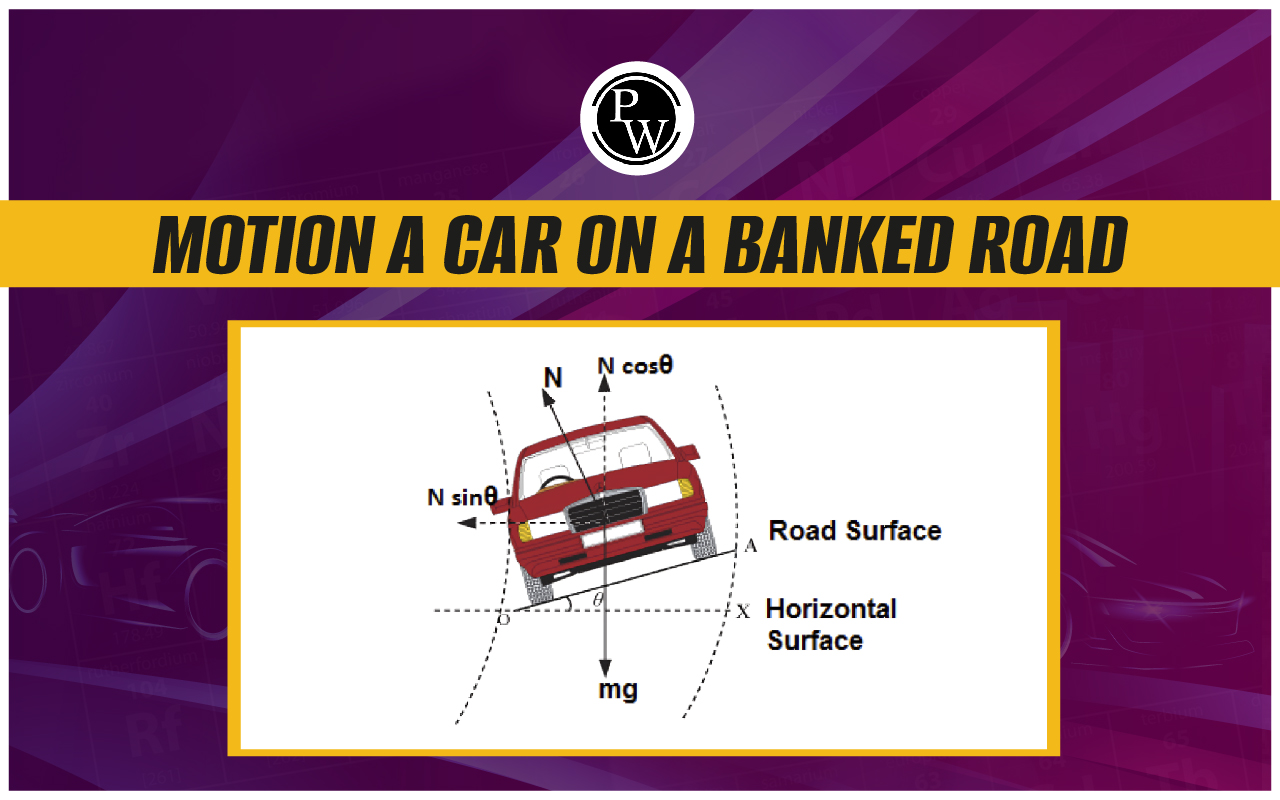
When vehicles go through turnings, they travel along a nearly circular arc. There must be some force which will produce the required acceleration. If the vehicle goes in a horizontal circular path, this resultant force is also horizontal. Consider the situation as shown in the figure.
A
vehicle of mass
M
moving at a speed
v
is making a turn on the circular path of radius
r
. The external forces acting on the vehicle are (i) weight Mg (ii) Normal contact force
N
and (iii) friction
f
s
.
If the road is horizontal, the normal force N is vertically upward. The only horizontal force that can act towards the center is the friction f
s
. This is static friction and is self-adjustable. The tyres get a tendency to skid outward and the frictional force which opposes this skidding acts towards the center. Thus, for a safe turn we must have
However, there is a limit to the magnitude of the frictional force. If s is the coefficient of static friction between the tyres and the road, the magnitude of friction fs cannot exceed sN. For vertical equilibrium
N
Mg
, so that
or
f
g
≤ μ
g
Mg
.
Thus, for a safe turn
Friction is not always reliable at circular turns if high speeds and sharp turns are involved. To avoid dependence on friction, the roads are banked at the turn so that the outer part of the road is somewhat lifted up as compared to the inner part.
The surface of the road makes an angle with the horizontal throughout the turn. The normal force
N
makes an angle with the vertical. At the correct speed, the horizontal component of
N
is sufficient to produce the acceleration towards the centre and the self-adjustable frictional force keeps its value zero. Applying Newton’s second law along the radius and the first law in the vertical direction,
and
These equations give.
The angle depends on the speed of the vehicle as well as on the radius of the turn. Roads are banked for the average expected speed of the vehicles. If the speed of a particular vehicle is a little less or a little more than the correct speed, the self-adjustable static friction operates between the tyres and the road, and the vehicle does not skid or slip. If the speed is too different from that given by equation even the maximum friction cannot prevent a skid or a slip.
If a vehicle is moving on a circular road which is rough and banked also, then three forces may act on the vehicle of these the first force, i.e. weight (
mg
) is fixed both in magnitude and direction. The direction of second force, i.e. normal reaction
N
is also fixed (perpendicular to the road) while the direction of the third force, i.e. friction
f
can be either inwards or outwards, while its magnitude can.
be varied from zero to a maximum limit,
f
L
=
µN
. So, the magnitude of normal reaction
N
and direction plus magnitude of friction f are so adjusted that the resultant of the three forces mentioned above is
mv
2
/
r
towards the centre. Of these m and r are also constant. Therefore, magnitude of
N
and direction plus magnitude of friction mainly depend on the speed of the vehicle
v
. Although situation varies from problem to problem yet, we can see that.
(i)
Friction f is upwards if the vehicle is at rest or v = 0. Because in this case the component of weight mg sin θ is balanced by f.
(ii)
Friction f is downwards if
v
>
(iii)
Friction f is upwards if
v
<
(iii)
Friction f is zero if
v
=
