Theorem 2

Lengths of two tangents drawn from an external point to a circle are equal.

Given: AP and AQ are two tangents drawn from a point A to a circle C (O, r).

To prove: AP = AQ.

Construction: Join OP, OQ and OA.

Proof: In ΔAOQ and ΔAPO

∠OQP = ∠OPA [Tangent at any point of a circle is perp. to radius through the point of contact]

AO = AO [Common]

OQ = OP [Radius]

So by R.H.S. criterion of congruency  Δ AOQ ≅ ΔAOP .

∴ AQ = AP. [By CPCT] Hence Proved

RESULT:

• If two tangents are drawn to a circle from an external point, then they subtend equal angles at the centre. ∠OAQ = ∠OAP [By CPCT].

• If two tanagents are drawn to a circle from an external point, they are equally inclined to the segment, joining the centre to that point ∠OAQ = ∠OAP [By CPCT].

question 1. If all the sides of a parallelogram touches a circle, show that the parallelogram is a rhombus.

Solution: Given: Sides AB, BC, CD and DA of a ||gm ABCD touch a circle at P,Q,R and S respectively.

To prove ||gm ABCD is a rhombus.

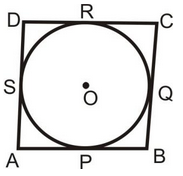
Proof : AP = AS .......(i)

BP = BQ .......(ii)

CR = CQ .......(iii)

DR = DS ........(iv)

[Tangents drawn from an external point to a circle are equal]

Adding (1), (2), (3) and (4), we get

⇒ AP + BP + CR + DR = AS + BQ + CQ + DS

⇒(AP + BP) + (CR + DR) = (AS + DS_ + (BQ + CQ)

⇒ AB + CD = AD + BC

⇒ AB + AB = AD + AD [In a ||gm ABCD, opposite side are equal]

⇒ 2AB = 2AD or AB = AD.

But AB = CD AND AD = BC [Opposite sides of a || gem]

∴ AB = BC = CD = DA.

Hence, ||gm ABCD is a rhombus.

question 2. From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.

Solution: Let O be the centre of the given circle and let P be a point such that OP = 10 cm.

Let PT be the tangent such that PT = 8 cm.

Join OT.

Now PT is a tangent at T and OT is the radius through T.

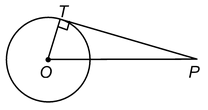
∴ OT ⊥ PT [Radius is ⊥ to tangent at the point of contact]

In the right ΔOTP, we have

OP ² = OT ² + PT ² [by Pythagoras' theorem]

⇒

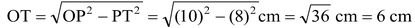
Hence, the radius of the circle is 6 cm.