Circles class 9 theorems

THEOREM9:

The sum of either pair of opposite angles of a cyclic quadrilateral is 180o.

Given :A cyclic quadrilateral ABCD.

To Prove :∠A + ∠C = ∠B + ∠D = 180 ^o

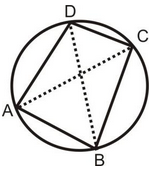
Construction :Join AC and BD.

Proof : ∠ACB = ∠ADB [Angles of same segment]

And ∠BAC = ∠BDC [Angles of same segment]

∴ ∠ACB + ∠BAC = ∠ADB + ∠BDC =∠ADC.

Adding ∠ABC to both sides, we get

∠ACB + ∠BAC + ∠ABC =∠ADC + ∠ABC.

The left side being the sum of three angles of ΔABC is equal to 180 ^o .

∴ ∠ADC + ∠ABC = 180 ^o

i.e., ∠D + ∠B = 180 ^o

∴ ∠A + ∠C = 360 ^o –(∠B + ∠D) = 180 ^o [∴∠A + ∠B + ∠C + ∠D = 360 ^o ]

Hence Proved.

Corollary :If the sum of a pair of opposite angles of a quadrilateral is 180o, then quadrilateral is cyclic.

question 15 In figure, ∠ABC = 69 ^o , ∠ACB = 31 ^o , find ∠BDC.

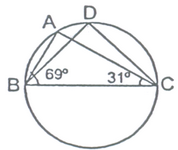
Solution: In ΔABC.

∠BAC + ∠ABC + ∠ACB = 180o

[Sum of all the angles of a triangle is 180 ^o ]

⇒ ∠BAC + 69 ^o + 31 ^o = 180 ^o

⇒ ∠BAC + 100 ^o = 180 ^o

⇒ ∠BAC = 180o– 100o = 80o

Now,∠BDC = ∠BAC = 80 ^o .

Ans.[Angles in the same segment of a circle are equal]

question 16 ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70o, ∠BAC is 30 ^o , find ∠BCD. Further, if B = BC, find ∠ECD.

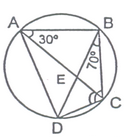
Solution: ∠CDB = ∠BAC = 30o ...(i) [Angles in the same segment of a circle are equal]

∠DBC = 70o ....(ii)

In ΔBCD,

∠BCD + ∠DBC + ∠CDB = 180 ^o [Sum of all he angles of a triangle is 180 ^o ]

⇒ ∠BCD + 70 ^o + 30 ^o = 180 ^o [Using (i) and (ii)]

⇒ ∠BCD + 100 ^o = 180 ^o

⇒ ∠BCD = 180 ^o – 100 ^o

⇒ ∠BCD = 80 ^o ...(iii)

In ΔABC,

AB = BC

∴ ∠BCA = ∠BAC = 30 ...(iv)[Angles opposite to equal sides of a triangle are equal]

Now,∠BCD = 80 ^o [From (iii)]

⇒ ∠BCA + ∠ECD = 80 ^o

⇒ 30o + ∠ECD = 80 ^o

⇒ ∠ECD = 80 ^o – 30 ^o

⇒ ∠ECD = 50 ^o

question 17 In the given figure, chord ED is parallel to the diameter AC of the circle. If ∠CBE = 650, then the value of ∠DEC is

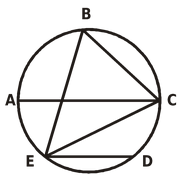
(a) 350 (b) 550 (c) 450 (d) 250

Solution: ∠EAC = ∠EBC = 650 (Angles in the same segment are equal)

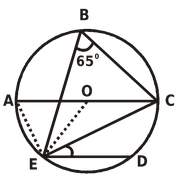
∠AEC = 900 (Angles in the semicircle)

In ∆ AEC, ∠EAC + ∠AEC + ∠ACE = 1800

650 + 900 + ∠ACE = 1800 ⇒∠ACE = 250

∠DEC = ∠ACE = 250 (∠DEC and ∠ACE are alternate angles as AC parallel to ED)

question 18 If the nonparallel side of a trapezium are equal, prove that it is cyclic.

Solution: Given :ABCD is a trapezium whose two non-parallel sides AB and BC are equal.

To Prove :Trapezium ABCD is a cyclic.

Construction :Draw BE ║ AD.

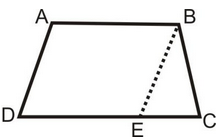
Proof: ∴ AB ║ DE [Given]

AD ║ BE [By construction]

∴ Quadrilateral ABCD is a parallelogram.

∴ ∠BAD = ∠BED ....(i) [Opp. angles of a║gm]

And,AD = BE ....(ii) [Opp. sides of a ║gm]

But AD = BC ...(iii) [Given]

From (ii) and (iii),

BE = BC

∴ ∠BEC = ∠BCE ....(iv) [Angles opposite to equal sides]

∠BEC + ∠BED = 180 ^o [Linear Pair Axiom]

⇒ ∠BCE + ∠BAD = 180 ^o [From (iv) and (i)]

⇒ Trapezium ABCD is cyclic.

[∴If a pair of opposite angles of a quadrilateral 180o, then the quadrilateral is cyclic]

Hence Proved.

question 19 Prove that a cyclic parallelogram is a rectangle.

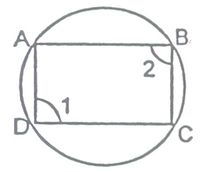
Solution: Given :ABCD is a cyclic parallelogram.

To Prove :ABCD is a rectangle.

Proof :∴ ABCD is a cyclic quadrilateral

∴ ∠1 + ∠2 = 180 ^o ....(i)

[∴Opposite angles of a cyclic quadrilateral are supplementary]

∴ ABCD is a parallelogram

∴ ∠1 = ∠2 ...(ii) [Opp. angles of a || gm]

From (i) and (ii),

∠1 = ∠2 = 90 ^o

∴ ||gm ABCD is a rectangle. Hence Proved.