Construction Of Tangents From A Point Outside The Circle

WHEN CENTRE IS GIVEN:

When point of tangency is on the circle.

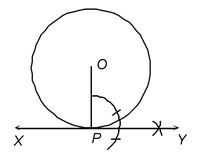
Given : A circle with centre O.

Required : To draw a tangent from point P on the circle.

Steps of construction:

1. Take a point O on the plane of the paper and draw a circle of given radius.

2. Take a point P on the circle.

3. Join OP.

4. Construct ∠OPX = 90°.

5. Produce XP to Y to get XPY as the required tangent.

When point of tangency is outside the circle

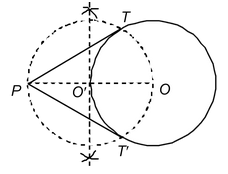
Given: A circle with centre O.

Required: To draw a tangent from an external point, i.e. P.

Steps of construction:

1. Join the centre O of the circle to the given external point, i.e. P.

2. Draw ⊥ bisector of OP, intersecting OP at O′.

3. Taking O′ as centre and OO′ = PO′ as radius, draw a circle to intersect the given circle at T and T′.

4. Join PT and PT′ to get the required tangents as PT and PT′.

WHEN CENTRE IS NOT GIVEN:

⇒ When point of tangency is on the circles.

Given: A circle and a point P on it.

Required: To draw a tangent at P without using centre of the circle.

Steps of construction:

1. Draw any chord PQ of the circle through P as in figure.

2. Take any point R on the major arc PQ and join PR and QR.

3. Construct ∠QPX equal to ∠PRQ.

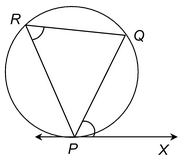
Then PX is the required tangent at P to the circle.

When point of tangency is outside the circle.

Given: A circle and a point P outside it.

Required: To draw a tangent from point P without using the centre.

Steps of construction:

1. Let P be the external point from where the tangents are to be drawn to the given circle.

2. Through P draw a secant PAB to intersect the circle at A and B.

3. Produce AP to a point C such that AP = PC.

4. Draw a semi-circle with BC as diameter.

5. Draw PD ⊥ CB, intersecting the semi-circle at D.

6. With P as centre and PD as radius draw arcs to intersect the given circle at T and T′.

7. Joint PT and PT′. PT and PT′ are the required tangents.

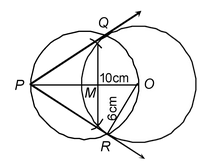
1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.

Solution: Given:

(i) A circle with centre O and radius 6 cm.

(ii) A point P at a distance of 10 cm from O.

Required: To draw two tangents to the circle from point P and measure the lengths of the tangents.

Steps of construction:

1. Bisect the line-segment OP. Let the point of bisection be M.

2. Taking M as centre and OM as radius, draw a circle. Let is intersect the circle at the points Q and R.

3. Join PQ and PR. These are the required tangents. On measuring, PQ = PR = 8 cm.

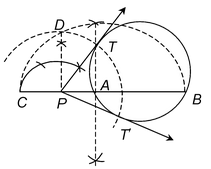
2. Draw tangents from an external point P to a circle of radius 4 cm without using the centre.

Solution: Given: A circle of radius 4 cm.

Required: To draw two tangents from an external point P.

Steps of construction:

1. Draw a circle of radius 4 cm.

2. Take a point P outside the circle and draw a secant PAB, intersecting the circle at A and B.

3. Produce AP to C such that PA = CP.

4. Draw a semi-circle with CB as diameter.

5. Draw PD ⊥ CB, intersecting the semi-circle at D.

6. With P as centre and PD as radius draw arcs to intersect the given circle at T and T′.

7. Join PT and PT′. Then PT and PT′ are the required tangents.

3. Draw a line segment AB of length 6 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle.

Sol. Steps of construction:

1. Draw a line segment AB = 6 cm.

2. With centre A and radius = 3 cm, draw a circle.

3. With centre B and radius = 2 cm, draw another circle.

4. With M, the midpoint of AB, as centre and radius AM = MB, draw the circle intersecting the circle of radius 3 cm at R and S and intersecting the circle of radius 2 cm at P and Q.

5. Join AP, AQ, BR and BS.

Then AP and AQ are tangents to the circle with centre B and radius 2 cm from point A

BR and BS are tangents to the circle with centre A and radius 3 cm from point B.

Justification :

Join AR.

∠ARB = 90 ^o [Angle in a semicircle]

i.e. BR is perpendicular to AR

Since AR is the radius of the circle with centre A and radius 3 cm, BR has to be a tangent to this circle.

Similarly BS is also a tangent this circle.

Join BP

∠BPA = 90 ^o [Angle in a semicircle]

i.e. AP is perpendicular to BP.

Since BP is the radius of the circle with centre B and radius 2 cm, AP has to be tangent to this circle.

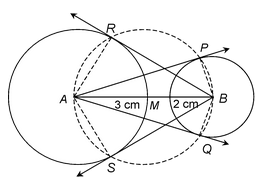
Similarly, AQ is also a tangent to this circle.

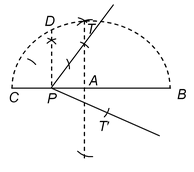
4. From a point P outside a circle of radius 2 cm, draw two tangents to the circle without using its centre.

Solution: Given: A circle of radius 2 cm and a point P outside the circle.

Required: To draw two tangents from P to the circle without using its centre.

Steps of construction:

1. Draw a secant PAB to the circle.

2. Draw XY, the perpendicular bisector of PB. Let it intersect PB at M.

3. With M as centre and radius equal to MP or MB, draw a semicircle.

4. Draw a line perpendicular to PB through A. Let it intersect the semicircle at the point C.

5. With P is as centre and PC as radius, draw arcs to intersect the given circle at two points, say Q and R.

6. Join PQ and PR.

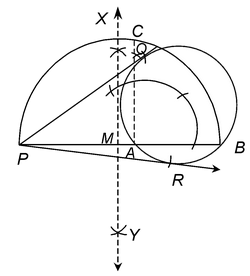
Then PQ and PR are the required tangents.

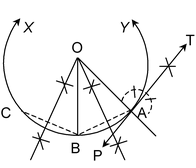
5. Draw a tangent from at point A on an arc.

Sol. Steps of Construction:

1. A is any point on arc XY.

2. Mark any two points B and C other than A on this arc.

3. Draw ⊥ bisectors of BC and AB which intersect each other at O.

4. Join OA. Draw ∠OAT = 90º.

5. PAT is the required tangent.