Centroid Of A Triangle

The point of intersection of the medians of a triangle is called the centroid of a triangle and it divides the median internally in the ratio 2 : 1.

Medians are the line coming from one vertex and bisecting the opposite side.

The coordinates of the centroid of a triangle with vertices 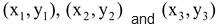is given by .

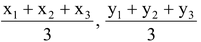Proof: Let 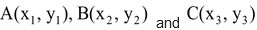be the vertices of a ΔABC.

Let D be the midpoint of BC.

Then the coordinates of D by midpoint formula are .

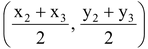Let G(x, y) be the centroid of ΔABC. Then G divides AD in the ratio 2 : 1.

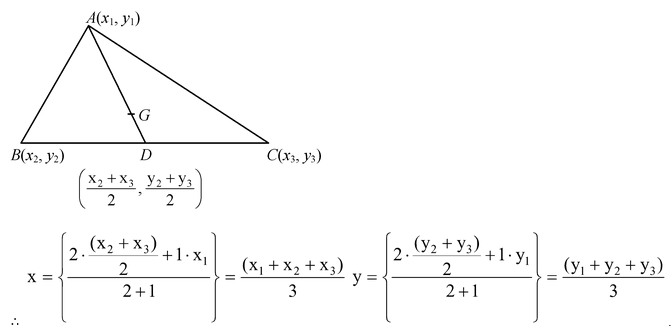
Hence the coordinates of G are .

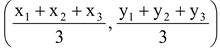Note : Centroid of the triangle obtained by joining the middle points of the triangle is same as the centroid of the original triangle.

question 1. Find the centroid of ΔABC whose vertices are A(–3, 0), B(5, –2) and C(–8, 5). And hence also find the centroid of a triangle having the midpoints as ?

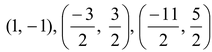Solution: Here,

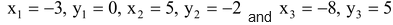
Let G(x, y) be the centroid of ΔABC. Then

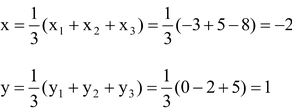
Hence, the centroid of ΔABC is G(–2, 1).

Again Let G(x,y)  be the centroid of ΔABC (by the help of the note in the previous page.)

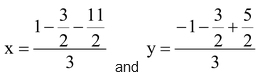. Hence the centroid is (-2,1).