Mechanism Of Current Flow In Metallic Conductors
Current Electricity of Class 12
MECHANISM OF CURRENT FLOW IN METALLIC CONDUCTORS
Flow of current in metals is due to flow of free electrons. In the absence of any externally applied emf (by means of a battery), the free electrons move randomly through the metal from one point to another giving zero net current.
When connected to a battery, the free electrons get accelerated due to the electric field (set up by the battery) and they gain velocity and energy. However, the passage is not smooth and the electrons collide with the lattice ions in which the ultimate gainer (of energy) is the ion. As we know the temperature of a body is related with the energy of vibrations of these ions, these collisions result in increase in temperature of the metal. The loss of energy of electrons in collision and their acceleration by the electric field, finally, results in drifting of electrons in a particular direction. (Although the actual motion of electrons is erratic, the overall effect is of drifting of electrons)
Drift Speed
|
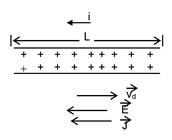
When no current flows through a conductor, its conduction electrons move randomly, with no net motion in any direction. When the conductor does have a current through it, these electrons still move randomly but now they tend to drift with a drift speed v d in the direction opposite to that of the applied electric field which causes the current. The drift speed is small compared to the speed of the random motion of the electrons. |
|
Let us assume that the positive charge carriers move with the same drift speed v d across the wire’s cross− sectional area A as shown in the figure.
The number of charge carriers in a length L of the wire is nAL, where n is the number of charge carriers per unit volume. The total charge of the carriers, each with charge e, in the length L is
q = (nAL)e
Since all charge carriers move along the wire with speed v d , therefore total charge moves through any cross section of the wire in the time interval,
t = L/vd
∴ Current (i) = q/t
or,i = nAev d
or ,v d = i/nAe
or,
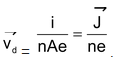 .
.
|
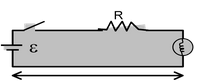
Exercise 2: A bulb is connected by a pair of long straight conductors of effective resistance R, with a source of e.m.f. ε. What time after turning on the switch the bulb glows and after what time the electrons from the source reaches the bulb? Answer it qualitatively. |
|
Illustration 4.What is the drift velocity of electrons in a copper conductor having a cross-sectional area of 5 × 10 − 6 m 2 , if the current is 10 A? Assume that there are 8 × 10 28 electrons/m 3 .
Solution:Given that,
A = 5 × 10 − 6 m 2 , I = 10 A, and n = 8 × 10 28 electrons / m 3
Now, v
d
=
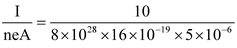 m/s
m/s
or, v d = 1.5625 × 10 − 4 m/s.
Illustration 5. A copper wire of cross−section 2 mm 2 carries a current of 30 A. Calculate the root-mean-square velocity (thermal velocity) of free electrons at 27 o C. Also prove that v d is very small compared to it.
Data given: ρ Cu = 8.9 gm/cc, Boltzmann constant k = 1.38 × 10 − 23 J/K
m e = 9.1× 10 − 31 kg, N A = 6.023 × 10 23 , Atomic weight of Cu = 63.
Solution:
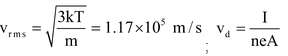
63 gm of Cu = 6.023 × 10 23 Cu atoms.
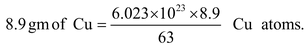 = 1 cc of Cu atoms.
= 1 cc of Cu atoms.
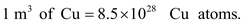
Now, each Cu atom contributes one electron
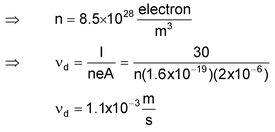
It is clear that v d is much smaller than v thermal .
Mobility
Mobility of a charge carrier is defined as the drift velocity of the charge carrier per unit electric field. It is generally denoted by μ. If v d is drift velocity attained by free electrons on applying electric field E, then electron mobility is given by.
μ = vd/E
The SI unit of μ is m 2 V − 1 s − 1 .
Substituting v d = μE in I = neAv d . We get I = neAμE. This equation gives the relation between electron mobility and the current through conductor.
Related Topics