System Of Variable Mass
Share
System Of Variable Mass
Impluse And Momentum of Class 11
So far we have dealt with the dynamics of a system whose mass is constant. We now wish to discuss the dynamics of a system, such as a rocket, whose mass varies. One may try to apply the following equation in such a case.
=
(9.27)
However, this equation is correct in only a few very special cases. This approach is not correct when mass actually enters or leaves the system.
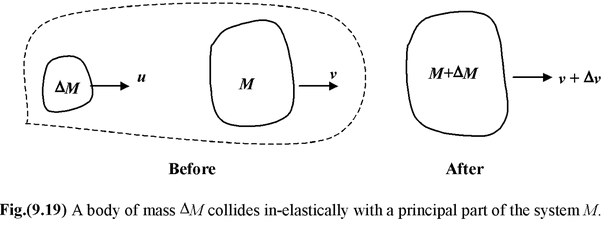
Let us examine the motion of a body of mass M, moving with velocity v. Another small body of mass ΔM approaches with velocity u along the same line. We assume u > v and that after the collision the two bodies stick together and move at velocity (v + Δv), as shown in the figure (9.19).
By defining the system comprises both the bodies we can use
=
, where
is the total momentum of the system of constant mass, M + ΔM. The change in momentum of the system in time Δt is
ΔP = (M + ΔM)(v + Δv) – Mv - ΔMu
= MΔv – (u – v)ΔM
Now (u – v) = vrel is the velocity of ΔM relative to M before the collision.
We divide both sides of this equation by Δt and take the limit as Δt → 0:
=
(9.28)
Note how equation (9.28) differs from equation (9.27), the sign of the second term is negative and
is replaced by
. The reason for this discrepancy is that the expression
for the total momentum is valid only if we take
to be
. In equation (9.27),
refers to the velocity of just the principal part of the system.
It is convenient to rewrite it in the form
=
+
dM/dt(9.29)
The acceleration
of the principal part, whose instantaneous mass is M, is determined.
∙By
, the net external force on the whole system (of constant mass M + ΔM), and
∙ by
, which is the rate at which momentum is being transferred into, or out, the principal part. It is also called the thrust force
=
dM/dt
Example 9.17
A hopper releases grain at a rate dm/dt onto a conveyor belt that moves at a constant speed v. What is the power of the motor driving the belt?
Solution
Let the system is some arbitrary length of belt whose mass we can call M. This mass of the system increases at the same rate that the grain falls,
so dM/dt = dm/dt.
Since the grain falls vertically,
= 0 and
=
-
= −
. Since the speed is constant,
dv/dt = 0. Thus from equation
0 =
, -
dm/dt
where
is the force needed to maintain constant speed because the mass is increasing. The power required (P = .
) is
P = v2
It is interesting to compare this with the rate at which the kinetic energy of the grain increases.
dK/dt = 1/2V 2 dm/dt
This is only half the power input. The other half is dissipated as heat when the grain lands on the belt and slips relative to it.
Related Topics
