ALGEBRAIC IDENTITY
Share
ALGEBRAIC IDENTITY
Polynomial of Class 9
ALGEBRAIC IDENTITY
An identity is an equality which is true for all values of the variables
Some important identities are
(i) (a + b) 2 = a 2 + 2ab + b 2
(ii) (a– b) 2 = a 2 – 2ab + b 2
(iii) a 2 – b 2 = (a + b) (a – b)
(iv) a 3 + b 3 = (a + b) (a 2 – ab + b 2 )
(v) a 3 – b 3 = (a – b) (a 2 + ab + b 2 )
(vi) (a + b) 3 = a 3 + b 3 + 3ab (a + b)
(vii) (a– b) 3 = a 3 – b 3 – 3ab (a – b)
(viii) a 4 + a 2 b 2 + b 4 = (a 2 + ab + b 2 ) (a 2 – ab + b 2 )
(ix) a 3 + b 3 + c 3 – 3abc = (a + b + c) (a 2 + b 2 + c 2 – ab – bc – ac)
Special case : if a + b + c = 0 then a 3 + b 3 + c 3 = 3abc.
(x) (a + b + c ) 2 = + a 2 + b 2 + c 2 +2ab +2bc +2ca
(xi) (a + b - c ) 2 = + a 2 + b 2 + c 2 +2ab -2bc - 2ca (Minus sign with c only)
(xii) (a - b - c ) 2 = + a 2 + b 2 + c 2 -2ab +2bc - 2ca (Minus sign with a only)
(a) Value Form :
(i) a2 + b 2 = (a + b) 2 – 2ab, if a + b and ab are given
(ii) a 2 + b 2 = (a – b) 2 + 2ab if a – b and ab are given
(iii) a + b =
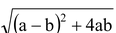if a – b and ab are given
(iv) a– b =
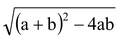if a + b and ab are given
(v) a
2
+
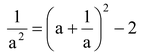if a +
1/a
is given
(vi) a
2
+
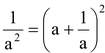+a – 1/a is given
(vii) a 3 + b 3 = (a + b) 3 – 3ab(a + b) if (a + b) and ab are given
(viii) a 3 – b 3 = (a – b) 3 + 3ab(a – b) if (a – b) and ab are given
(ix)
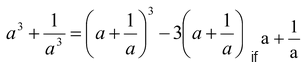
(x)
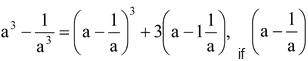
(xi) a 4 + b 4 = (a 2 + b 2 ) 2 – 2a 2 b 2 = [(a + b) 2 – 2ab] 2 – 2a 2 b 2 , if (a + b) and ab are given
(xii) a 2 – b 2 = (a 2 + b 2 ) (a 2 – b 2 ) = [(a + b) 2 – 2ab](a + b) (a – b)
(xiii) a 5 + b 5 = (a 3 + b 3 ) (a 2 + b 2 ) – a 2 b 2 (a + b)
ZEROS OF A POLYNOMIALS :
Zero of the polynomial is define as the value of the variable satisfy the polynomial .
(i) f (x) = 5x 3 – 2x 2 + 3x – 2
If x = 1, then f(1) = 5 × (1) 3 – 2 × (1) 2 + 3 × (1) – 2 = 5 – 2 + 3 – 2
f(1) = 4
Similarly, f(0) = 5 × (0) 3 – 2 × (0) 2 + 3 × (0) – 2
f(0) = –2
Again, f(–1) = 5 × (–1) 3 – 2(–1) 2 + 3(–1) – 2 = –5 – 2 – 3 – 2
f(–1) = –12
(ii) p(x) = 2x 3 + x 2 – 2x – 1
If x = –1, then p(–1) = 2 × (–1) 3 + (–1) 2 – 2 × (–1) – 1
= –2 + 1 + 2 – 1 = 0.
Things to remember
(i) Every real number is a zero of the zero polynomial
(ii) A zero of a polynomial need not be 0
(iii) 0 may be a zero of a polynomial
(iv) Every linear polynomial has one and only one zero
(v) A polynomial can have more than one zero.
question What is the zero of the polynomial p(x) = 2x – 3r.
Solution: For zero of polynomial put p(x) = 0
i.e. 2x – 3r = 0
or 2x = 3r
x = 3r/2
question
Find zeros of the polynomial
.
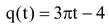Solution: Zeros of polynomial q(t) = 3πt – 4 is q(t) = 0
or 3πt – 4 = 0
3πt = 4
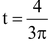
question Find the value of each of the following polynomials at the indicated value of variables:
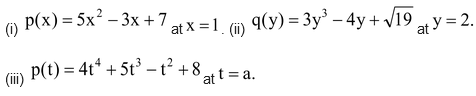
question Find the value of:
(i) 36x2 + 49y 2 + 84xy, when x = 3, y = 6
(ii) 25x 2 + 16y 2 - 40xy, when x = 6, y = 7
Sol. (i) 36x 2 + 49y 2 + 84xy = (6x) 2 + (7y) 2 + 2 × (6x) × (7y)
= (6x + 7y) 2
= (6 × 3 + 7 × 6) 2 [When x = 3, y = 6]
= (18 + 42) 2
= (60) 2
= 3600. Ans.
(ii) 25x 2 + 16y 2 – 40xy = (5x) 2 + (4y) 2 – 2 × (5x) × (4y)
= (5x – 4y) 2
= (5 × 6 – 4 × 7) 2 [When x = 6, y = 7]
= (30 - 28) 2
= 22
= 4 Ans.
