Fluid Statics
Solids And Fluids of Class 11
Fluid Statics
It refers to the state when there is no relative velocity between fluid elements. In this section we will learn some of the properties of the fluid statics.
Variation of Pressure with Depth
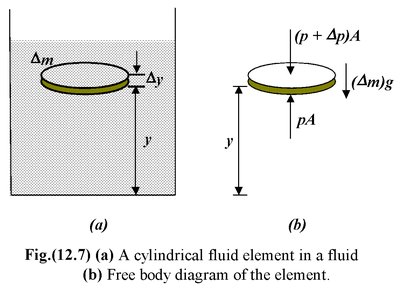
Consider a small cylindrical element of mass Δm at a height y from the base of the container as shown in the figure (12.7 a). Let A be the area of the top and bottom surface of this cylinder.
We know that the fluid forces on the opposite vertical faces of the cylinder are equal in magnitude and opposite in direction, and therefore, cancel. The other forces acting on the fluid contained within the imaginary boundary is the gravitational force
|
ΔW = (Δm)g and the forces due to fluid pressure. The pressure force acting on the lower face of the element is pA and that on the upper face is (p + Δp)A. The fig.(12.7 b) shows the free body diagram of the element. Applying the condition of equilibrium we get, pA – (p + Δp)A – (Δm)g = 0 |
|
If ρ be the density of the fluid at the position of the element, then Δm = ρA(Δy)
andpA – (p + Δp)A - ρgA(Δy) = 0
or Δp/Δy = -ρg
In the limit as approaches to zero, Δp/Δy becomes
|
dp/dy = -ρg (12.14) The above equation indicates that the slope of p versus y is negative. That is, the pressure p decreases with height y from the bottom of the fluid. In otherwords, the pressure p increases with depth h, i.e. dp/dh = ρg (12.15) |
|
The Incompressible Fluid Model
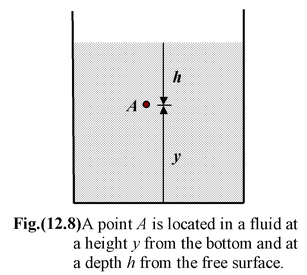
For an incompressible fluid, the density ρ of the fluid remains constant throughout its volume. It is a good assumption for liquids. To find pressure at the point A in a fluid column as shown in the figure(12.8) is obtained by integrating equation (12.15).
dp = ρgdh
or
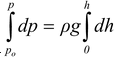
or p – p o = ρgh
or p = p o + ρgh(12.16)
whereρ is the density of the fluid, and
p o is the atmospheric pressure at the free surface of the liquid.
Absolute Pressure and Gauge Pressure
Absolute pressure is the total pressure at a point while gauge pressure is relative to the local atmospheric pressure. Gauge pressure may be positive or negative depending upon the fact whether the pressure is more or less than the atmospheric pressure.
pgauge = pabsolute – patm(12.17)
Pascal Law
According to equation (12.16),
p = p o + ρgh
pressure at any depth h in a fluid may be increased by increasing the pressure po at the surface. Pascal recognized a consequence of this fact that we now call Pascal’s Law.
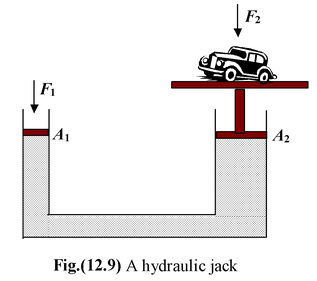
A pressure applied to a confined fluid at rest is transmitted equally undiminished to every part of the fluid and the walls of the container.
This principle is used in a hydraulic jack or lift, as shown in the figure.
The pressure due to a small force F1 applied to a piston of area A1 is transmitted to the larger piston of area A2. The pressure at the two pistons is the same because they are at the same level.
|
p =
or F
2
=
Consequently, the force on the larger piston is large. Thus, a small force F1 acting on a small area A1 results in a larger force F2 acting on a larger area A2. |
|
|
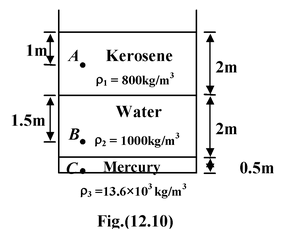
Example: 12.7 Find the absolute pressure and gauge pressure at points A, B and C as shown in the figure(12.10). (1 atm = 105 Pa) |
|
Solution
patm = 10 5 Pa
|
Points |
Gauge Pressure |
Absolute Pressure |
|
A |
pA = ρ1ghA = (800)(10)1 = 8 kPa |
p′A = pA + patm = 108 kPa |
|
B |
pB = ρ1g(2) + ρ2g(1.5) = (800)(10)(2) + (103)(10)(1.5) = 31 kPa |
p′B = pB + patm = 131 kPa |
|
C |
pC = ρ1g(2) + ρ2g(2) + ρ3g(0.5) = (800)(10)(2) + (103)(10)(2) + (13.6 × 103)(10)(0.5) = 104 kPa |
p′C = pC + patm = 204 kPa |
Example: 12.7
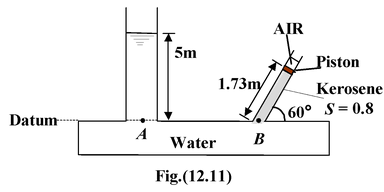
Find the pressure in the air column at which the piston remains in equilibrium. Assume the piston to be massless and frictionless.
Solution
|
Let pa be the air pressure above the piston. Applying Pascal’s law at points A and B. patm + ρwg(5) = pa + ρkg(1.73)sin60° pa = (103) (10)(5) + 105 - (800)(10)(1.73) = 138 kPa |
|
Example: 12.8
|
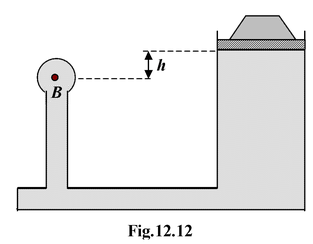
A weighted piston confines a fluid of density ρ in a closed container, as shown in the figure(12.12). The combined weight of piston and weight is W = 200 N, and the cross-sectional area of the piston is
|
|
Solution
Notice what Pascal’s principle tells us about the pressure applied to the fluid by the piston and atmosphere. This added pressure is applied at all points within the fluid. Therefore, the total pressure at B is composed of three parts:
Pressure of atmosphere = 1.0 × 105 Pa
Pressure due to piston and weight =
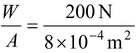 = 2.5 × 10
5
Pa
= 2.5 × 10
5
Pa
Pressure due to height h of fluid = hρg = 0.33 × 10 5 Pa
In this case, the pressure of the fluid itself is relatively small. We have
Total pressure at B = 3.8 × 105Pa = 380 kPa
The gauge pressure does not include atmospheric pressure. Therefore,
Gauge pressure at B = 280 kPa
|
Example: 12.9
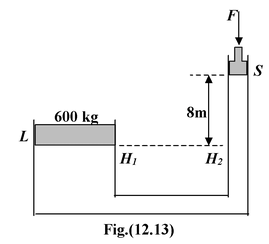
For the system shown in figure, the cylinder on the left, at L, has a mass of 600 kg and a cross-sectional area of
|
|
Solution
The pressures at point H1 and H2 are equal because they are at the same level in the single connected fluid. Therefore,
Pressure at H1 = Pressure at H2
(Pressure due to left piston) = (Pressure due to F and right piston) + (pressure due to 8 m of oil)
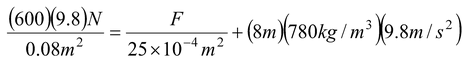
After solving, we get, F = 31 N.
The Compressible – Fluid Model
For gases, the constant density assumed in the compressible model is often not adequate. However, an alternative simplifying assumption can be made that the density is proportional to the pressure, i.e.,
ρ = kp
Let ρo be the density of air at the earth’s surface where the pressure is atmospheric po, then
ρo = kpo
After eliminating k, we get
ρ =
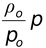
Substituting the value of ρ in equation (12.14),
dp = -ρgdy
or dp =
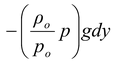
On rearranging, we get
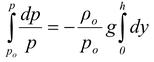
where p is the pressure at a height y = h above the earth’s surface.
After integrating, we get
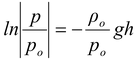
or p =
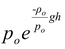 (12.19)
(12.19)
Note that instead of a linear decrease in pressure with increasing height as in the case of an incompressible fluid, in this case pressure decreases exponentially.

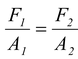
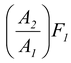 (12.18)
(12.18)