The Equation of Continuity
Solids And Fluids of Class 11
The Equation of Continuity
In order to describe the motion of a fluid, in principle one might apply Newton’s laws to a particle (a small volume element of fluid) and follow its progress in time. This is a difficult approach. Instead, we consider the properties of the fluid, such as velocity and pressure, at fixed points in space.
In order to simplify the discussion we make several assumptions:
(i) The fluid is non viscous
There is no dissipation of energy due to internal friction between adjacent layer in the fluid.
(ii)The flow is steady
The velocity and pressure at each point are constant in time
(iii)The flow is irrotational:
A tiny paddle wheel placed in the liquid will not rotate.
In rotational flow, for example, in eddies, the fluid has net angular momentum about a given point.
|
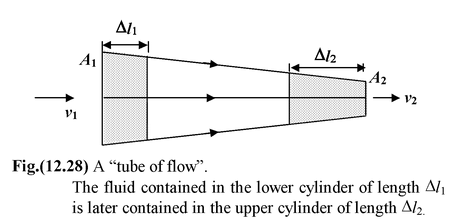
In general, the velocity of a particle will not be constant along a streamline. The density and the cross-sectional area of a tube of flow will also change. Consider two sections of a tube of flow, as shown in figure(12.28). The mass of fluid contained in a small cylinder of length Δl1 and area A1 is Δm1 = ρ1A1Δl1. |
|
Since fluid does not leave the tube of flow, this mass will later pass through a cylinder of length Δl2 and area A2. The mass in this cylinder is Δm2 = ρ2A2Δl2. The lengths Δl1 and Δl2 are related to the speeds at the respective locations: Δl1 = v1Δt and Δl2 = v2Δt. Since no mass is lost or gained.
Δm 1 = Δm 2 , and
ρ1A 1 v 1 = ρ 2 A 2 v 2 (12.28)
This is called the equation of continuity. It is a statement of the conservation of mass.
If the fluid is incompressible, its density remains unchanged. This is a good approximation for liquid, but not for gases. If ρ1 = ρ2, the equation (12.28) becomes,
A 1 v 1 = A 1 v 2 (12.29)
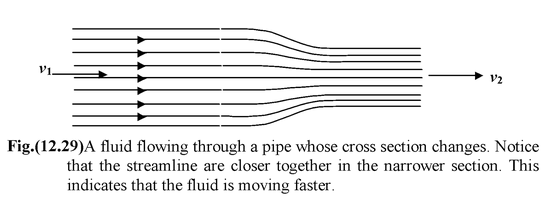
The product Av is the volume rate of flow (m3/s). Figure(12.29) shows a pipe whose cross section narrows. From equation (12.29) we conclude that the speed of a fluid is greatest where the cross-sectional area is the least. Notice that the streamlines are close together where the speed is higher.