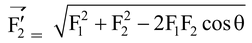Laws of Addition of Vectors
Vector of Class 11
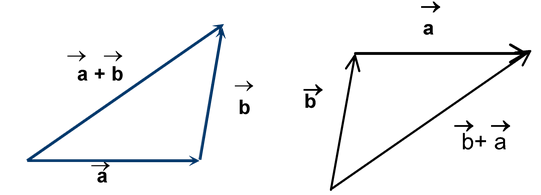
Two or more vectors can be added to give another vector, which is called the resultant of the vectors. The resultant would produce the same effect as that of the original vectors together.
(I)Geometrical method:
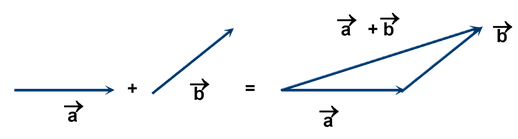
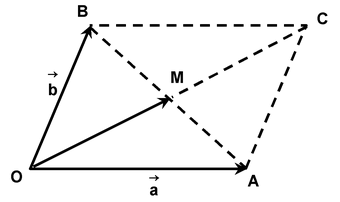
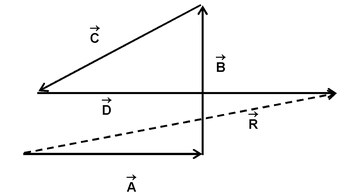
To find
 +
+
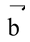 , shift
, shift
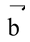 such that its initial point coincides with the terminal point of
such that its initial point coincides with the terminal point of
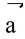 . Now, the vector whose initial point coincides with the initial point of
. Now, the vector whose initial point coincides with the initial point of
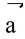 , and terminal point coincides with the terminal point of
, and terminal point coincides with the terminal point of
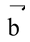 represents (
represents (
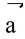 +
+
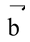 ) as shown in the above figure.
) as shown in the above figure.
To find (
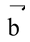 +
+
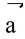 ), shift
), shift
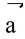 such that its initial point coincides with the terminal point of
such that its initial point coincides with the terminal point of
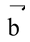 . A vector whose initial point coincides with the initial point of
. A vector whose initial point coincides with the initial point of
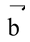 and terminal point coincides with the terminal point of
and terminal point coincides with the terminal point of
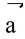 represents (
represents (
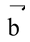 +
+
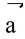 ).
).
|
Illustration 1. If the position vector of point A and B are
Solution:
|
|
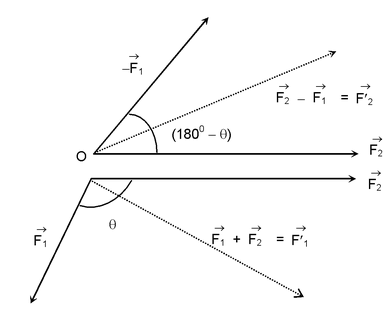
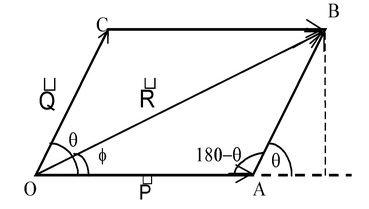
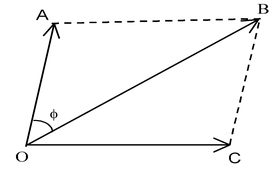
(II)Parallelogram law of addition of vectors:
If two vectors are represented in magnitude and direction by the two adjacent sides of a parallelogram drawn from a point, their resultant will be represented in magnitude and direction by the diagonal of the parallelogram drawn from that point.
|
We get , R 2 = P 2 + Q 2 + 2PQ cosθ
φ = tan-1
where φ is the angle that the resultant makes with
(i) θ = 0 0 |
|
 and
and
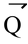 are in the same direction i.e. they are parallel cos 0
0
= 1
are in the same direction i.e. they are parallel cos 0
0
= 1
∴ |
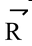 | = |
| = |
 | + |
| + |
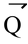 | & φ = 0
0
| & φ = 0
0
(ii) θ = 180
0
,
 and
and
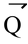 are in opposite direction i.e. they are antiparallel cos180
0
= -1
are in opposite direction i.e. they are antiparallel cos180
0
= -1
∴ |
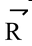 | = |
| = |
 | ~ |
| ~ |
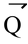 | and
| and
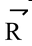 is in the direction of the larger vector.
is in the direction of the larger vector.
(iii) θ = 90 o , cos 90 0 = 0
 and
and
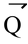 are perpendicular to each other
are perpendicular to each other
∴ |
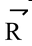 | = ( |
| = ( |
 |2 + |
|2 + |
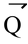 |2)1/2 & φ= tan-1(Q/P)
|2)1/2 & φ= tan-1(Q/P)
|
(III) Polygon law of addition of vectors:
Vectors obey commutative law
i.e.
|
|
Illustration 2. Two forces of 60N and 80N acting at an angle of 60 0 with each other, pull an object. What single pull would replace the given forces?
|
Solution: Two forces are drawn from a common origin O, making an angle of 60 0 . OA and OC represent the forces 60N and 80N respectively. The diagonal OB represents the resultant R. |
|
∴ R 2 = 60 2 + 80 2 + 2.60.80 cos 60 0
= 3600 + 6400 + 4800 = 14800 ∴ R = 121.7N
Angle φ is given, tanφ =
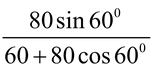
Which gives, φ = 34.70
Illustration 3. The resultant of two vectors 3P and 2P is R. If the first vector is doubled, the resultant vector also becomes double. Find the angle between the vectors.
Solution: Let θ be the angle between vectors, then
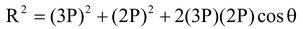
= 13P 2 + 12P 2 cos θ …(1)
Also (2R) 2 = (6P) 2 + (2P) 2 + 2(6P) (2P) cos θ
R 2 = 10P 2 + 6P 2 cos θ …(2)
From (1) and (2)
cos θ = − 1/2
∴ θ = 120°
Illustration 4. The sum of magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. The resultant is at 90° with the force of smaller magnitude. What are the magnitude of individual forces.
Solution: Let
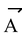 and
and
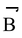 be two forces
be two forces

Exercise 1:
i) Is it possible that the resultant of two equal forces is equal to one of the forces?
ii) If a vector has zero magnitude is it meaningful to call it a vector?
iii) Can three vectors, not in one plane, give a zero resultant? Can four vectors do?
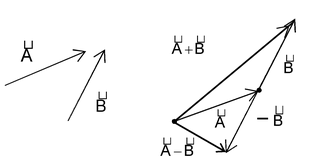
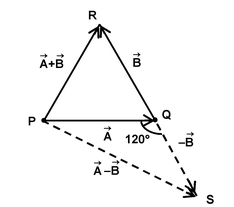
Subtraction of Vectors:
When a vector B is reversed in direction, then the reversed vector is written as -
|
|
Illustration 5.
If the sum of two unit vectors
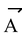 and
and
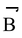 is also equal to a unit vector, find the magnitude of the vector
is also equal to a unit vector, find the magnitude of the vector
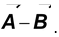 .
.
|
Solution:
Given that
Hence the angle between
Now,
|
|
|
Illustration 6. Two forces of unequal magnitudes simultaneously act on a particle making an angle
θ = 1500 with each other. If one of them is reversed, the acceleration of the particle is doubled. Calculate the ratio of the magnitude of the forces.
|
Solution: Let the two forces be forces
Using parallelogram law of vector addition, we get,
|
|
Since force is directly proportional to acceleration,
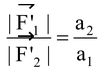
Substituting |
 |, |
|, |
 | and a2/a1 = 2/1, we have,
| and a2/a1 = 2/1, we have,
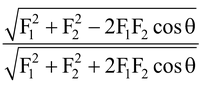 = 2
= 2
Substituting θ = 1500 and solving the quadratic equation, we have
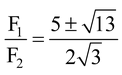
Illustration 7.
The resultant of
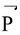 and
and
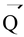 is
is
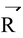 . If
. If
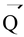 is doubled,
is doubled,
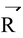 is doubled; when
is doubled; when
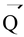 is reversed,
is reversed,
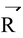 is again doubled, find P : Q : R.
is again doubled, find P : Q : R.
Solution:
Let θ be the angle between
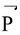 and
and
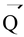 . Then
. Then
R2 = |
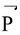 +
+
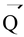 |2 = P2 + Q2 + 2PQ cos θ … (i)
|2 = P2 + Q2 + 2PQ cos θ … (i)
If
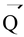 is doubled,
is doubled,
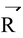 is doubled. That means, the magnitude of resultant of 2
is doubled. That means, the magnitude of resultant of 2
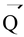 and
and
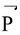 is 2R
is 2R
(2R) 2 = P 2 + (2Q) 2 + 2P(2Q) cos θ
This yields, 4R 2 = P 2 + 4Q 2 + 4PQ cos θ
When
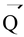 is reversed,
is reversed,
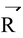 is doubled. Hence, the magnitude of resultant
is doubled. Hence, the magnitude of resultant
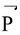
and (-
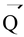 ) is 2R.
) is 2R.
Then, (2R) 2 = P 2 + Q 2 + 2PQ cos (!800 - θ).
This yields, 4R 2 = P 2 + Q 2 – 2PQ cosθ … (iii)
eq. (i) – eq(iii) gives PQ cos θ =
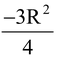 … (iv)
… (iv)
eq. (i) + eq (iii) gives P 2 + Q 2 = 5R2/2 …(v)
eq. (ii) + eq (iv) gives P 2 + 4Q 2 = 7R 2
solving eq. (v) and eq(vi) we obtain Q =
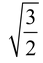 R and P = R
R and P = R
Hence P : Q : R =
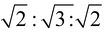

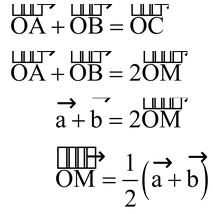
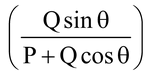
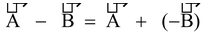
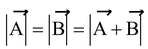 = 1
= 1
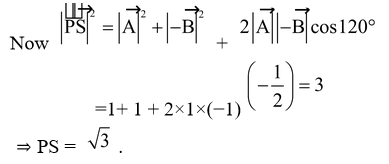
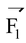 and
and
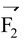 . The resultant of these forces. is
. The resultant of these forces. is
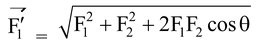 If the direction of
If the direction of