Work Energy Theorem
Work Power And Energy of Class 11
Let us study which physical quantity changes when work is done on a particle. If a constant force
F acts through a displacement x, it does work W = Fx = (ma) x on the particle.
Since the acceleration is constant, we can use the equation of kinematics
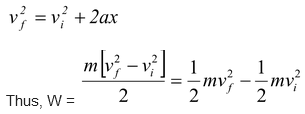 (8.9)
(8.9)
The quantity
K = 1/2mv 2
is a scalar and is called the kinetic energy of the particle.
Kinetic energy is the energy that a particle posses by virtue of its motion.
Thus, the equation (8.9) takes the form
W = Kf - Ki = ΔK (8.10)
The work done by a force changes the kinetic energy of the particle. This is called the
Work-Energy Theorem.
In general
The net work done by the resultant of all the force acting on the particle is equal to the change in kinetic energy of a particle.
Wnet = ΔΚ (8.11)
Important
(i)The kinetic energy of an object is a measure of the amount of work needed to increase its speed from zero to a given value.
(ii)The kinetic energy of a particle is the work it can do on its surroundings in coming to rest.
(iii)Since the velocity and displacement of a particle depend on the frame of reference, the numerical values of the work and the kinetic energy also depend on the frame.
|
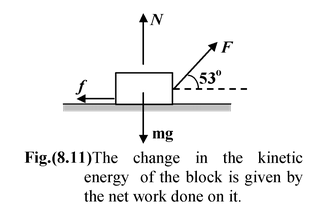
Example: 8.4 A block of mass m = 4 kg is dragged 2m along a horizontal surface by a force F = 30 N acting at 53o to the horizontal. The initial speed is 3 m/s and μk = 1/8. (a)Find the change in kinetic energy of the block (b)Find its final speed |
|
Solution
(a)The forces acting on the block are shown in the figure(8.11). Clearly, WN = 0 and Wg = 0, whereas WF = Fs cosθ
Wf = -fs = -μkNs where N = mg - Fsinθ
The work-energy theorem,
ΔK = Wnet = WF + Wf
therefore,
ΔK = F s cosθ - μk(mg – F sinθ)s
= (30)(2)(0.6) - 1/8 (40– 24)(2) = 32 J
(b)Now ΔK =
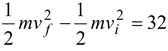 J
J
Since vi = 3 m/s.
therefore, vf = 5 m/s
Example: 8.5
|
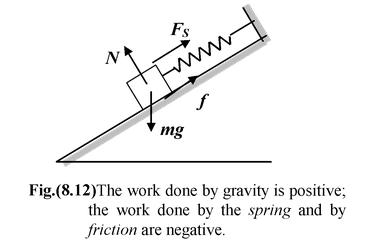
A block of mass m = 2 kg is attached to a spring whose spring constant is k = 8 N/m. The block slides on an incline for which μk = 1/8 and θ = 37 o . If the block starts at rest with the spring unextended, what is its speed when it has moved a distance d = 0.5m down the incline? |
|
Solution
This problem can be solved by using Newtons’s second law. However, the force exerted by the spring varies with position and, therefore, so does the acceleration. We avoid this difficulty by using the work-energy theorem. (Unless you are solving a problem in static equilibrium, it is a good idea to think of the energy approach rather than dynamics when you see a spring in problem.)
The work done by the force due to the spring was found in equation (8.8).
xi = 0 and xf = +d
The work done by each of the forces on the block are
Wg = +mgd sinθ
Wf = μkNd = −μk(mg cosθ)d
Ws = - 1/2kd 2
Of course, WN = 0. The work-energy theorem, with ΔK = 1/2mv 2 - 0, tells us
mgd sinθ - μk(mg cosθ) d - 1/2kd 2 = 1/2mv 2
putting m = 2 kg; d = 0.5 m; k = 8 N/m; sinθ = 3/5; cosθ = 4/5; μk = 1/8
we get , (2)(10)(0.5)(0.6) - 1/8 (20)(0.8)(0.5) - 1/2(8)(0.5) 2 = 1/2(2)v2
v = 2 m/s
Example: 8.6
|
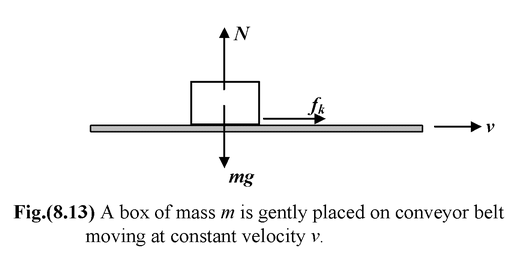
A box of mass m is gently placed on a conveyor belt that moves at a constant speed v. The coefficient of kinetic friction is μk. (a)What is the work done by friction? (b)How far does the box move before reaching its final speed? (c)When the box reaches its final speed, how far has the belt moved? |
|
Solution
(a)When the box is first placed on the belt there will be slipping between the two. But the force of friction on the box and its displacement are in the same direction. Consequently, the work done by kinetic friction is positive. Since the final speed of the box is v,
Wf = ΔK = + 1/2mv 2 (i)
(b)The force of friction is f = μkN = μkmg and Wf = +fd.
Thus from equation (i),
+μk mgd = +1/2mv 2 (ii)
Thus,d = v 2 / 2μk g
(c)If the box takes a time t to reach speed v, then v = at where a is the acceleration of box.. In this time it will move d = 1/2at 2 = 1/2 vt. Since the belt’s speed is fixed, in time t it moves a distance vt = 2d.
The belt moves twice as far as the box while the box is accelerating.
Example: 8.7
A horizontal force F very slowly lifts the bob of a simple pendulum from a vertical position to a point at which the string makes an angle θo to the vertical. The magnitude of the force is varied so that the bob is essentially in equilibrium all times.
What is the work done by the force on the bob?
Solution
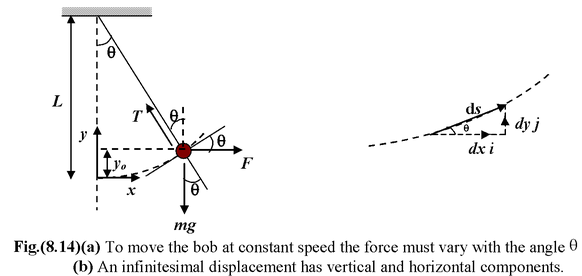
Figure (8.14) is a free body diagram of the system and shows the forces acting on the bob. Since the acceleration is zero, both the vertical and horizontal components of the forces balance:
ΣFx = F – T sinθ = 0
ΣFy = Tcosθ - mg = 0
Eliminating T we get
F = mg tanθ (i)
This is how the force must vary as a function of angle θ in order for the bob to be in equilibrium.
The work done by
![]() in an infinitesimal displacement
in an infinitesimal displacement
![]() along the circular arc is
along the circular arc is
dW =
![]() .
.
![]() = Fx dx
= Fx dx
= mg tanθ dx (ii)
From figure(8.14), w see that dy/dx = tanθ; thus, dy = tanθ dx.
Equation (ii) becomes dW = mg dy, therefore, the total work done from y = 0 to y = yo is
W =
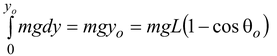
where the vertical displacement is
yo = L(1 – cosθ o ).