
In mathematics, Division Formula is one of the four fundamental arithmetic operations. The choice of which operation to use depends on the specific problem or requirement at hand. For instance, when the task is to distribute 100 chocolates equally among 25 children, the operation chosen is division. By dividing 100 by 25, it is determined that each child will receive 4 chocolates.
In this article, we will focus on one of these arithmetic operations, namely "Division" or "Divide." We will explore various aspects of the division Formula, including its symbol, the division math formula, the division of fractions, handling decimals in the division, the division of polynomials, and more. The article will feature a range of solved examples to illustrate the principles and applications of division in different mathematical contexts.
Division Formula Meaning
The term "divide" in mathematics refers to the act of separating a quantity or object into two or more equal parts, areas, classes, categories, groups, or divisions. In simpler terms, division entails distributing a whole entity into equal parts or creating equal divisions. For example, when a diagonal line is drawn across a square, it divides the square into two triangles, each having an equal area.
It's important to note that the result of a division Formula operation may or may not be an integer. In many cases, division will yield a quotient in the form of decimal numbers, especially when the dividend is not perfectly divisible by the divisor. Decimal quotients are common outcomes in division, and they represent the fractional part or the remainder when a quantity is divided into equal parts.
Division Formula Symbol
The symbol used to represent the operation of division Formula is typically "÷," a forward slash "/", or a horizontal line "_." These division Formula symbols are commonly used in mathematical notation to perform division in various types of problems and calculations. Additionally, expressions like "x/y" or "x ÷ y" can be read as "x by y" or "x over y."
For example, consider the division of 60 by 5. It can be represented in several ways:
60 ÷ 5 = 12
60/5 = 12
60_5 = 12
All three representations yield the same result of 12, highlighting the equivalence of these notations in denoting the division operation.
Division Formula
In the division Formula operation, there are four key terms to be aware of: dividend, divisor, quotient, and remainder. The formula to calculate the division of two numbers is expressed as:
Dividend ÷ Divisor = Quotient + Remainder.
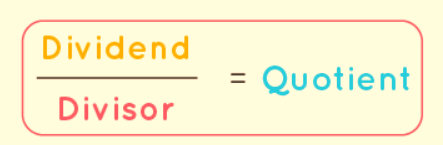
Here's what each of these terms represents:
The dividend is the number being divided.
The divisor is the number that divides the dividend into equal parts.
The quotient is the result of the division operation.
The remainder is the leftover number in the division operation, which indicates what is left when the dividend is not perfectly divisible by the divisor.
For example, in the division 46 ÷ 5:
46 is the dividend.
5 is the divisor.
The quotient is 9.
The remainder is 1.
Here are some important points to remember regarding division:
When a number is divided by 1, the answer should be the same as the dividend. For example, 56 ÷ 1 is 56.
If the dividend and divisor are the same, the quotient is 1. For example, 10 ÷ 10 is 1.
Division by 0 is undefined. If the divisor is 0, the answer is undefined. For example, 15 ÷ 0 is undefined.
Division Formula Problems
Division is indeed one of the fundamental arithmetic operations used for a wide range of mathematical problems and expressions. Here are a few division problems along with their solutions:
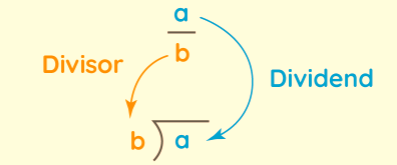
Divide 375 by 5:
375 ÷ 5 = 75
Divide 226 by 4:
226 ÷ 4 = 56.5
Divide 784 by 14:
784 ÷ 14 = 56
Division is a versatile operation used to solve a variety of mathematical problems and can involve different types of numbers, expressions, and variables.
Division Formula Fractions
We can also perform division formula operations on fractions. While dividing fractions, the division operator needs to be converted into multiplication. This can be understood in a better way using the example given below:
Divide 2/3 by 4/5:
Numerator = ⅔
Denominator = ⅘
Thus, (⅔)/ (⅘)
This can be written as:
(2/3) × (5/4)
= (1/3) × (5/2)
= 5/6
Therefore, (⅔)/ (⅘) = 5/6
Division Formula Decimals
Dividing decimals is similar to dividing whole numbers, with one important rule: you need to make sure that the divisor (the number you're dividing by) is a whole number. Here's a step-by-step guide on how to divide decimals:
Step 1: Ensure the divisor is a whole number.
If the divisor is not a whole number, move the decimal point to the right until it becomes a whole number. Do the same to the dividend (the number you're dividing) to keep the value the same.
Step 2: Divide as you would with whole numbers.
Perform the division as you would with whole numbers, ignoring the decimal point.
Step 3: Place the decimal point.
After you've divided the numbers as whole numbers, count the total decimal places in both the dividend and divisor.
Step 4: Place the decimal point in the quotient.
Place the decimal point in the quotient so that it has the same number of decimal places as the total from step 3.
Here's an example:
Divide 3.6 by 0.2:
Step 1: Ensure the divisor is a whole number.
Divisor: 0.2 (move the decimal point one place to the right)
Dividend: 3.6 (move the decimal point one place to the right)
Now we have 36 divided by 2.
Step 2: Divide as you would with whole numbers.
36 ÷ 2 = 18
Step 3: Count total decimal places.
Dividend: 3.6 (1 decimal place)
Divisor: 0.2 (1 decimal place)
Step 4: Place the decimal point.
Place the decimal point in the quotient to have the same number of decimal places as the total from step 3, which is one.
So, the result is 18.0, or simply 18.
That's how you divide decimals. Remember to make sure the divisor is a whole number, perform the division as you would with whole numbers, and then place the decimal point in the quotient.
Divide the decimal 0.256 by 0.08:
0.256/0.08
First, we have to express the given decimals in terms of fractions as:
0.256 = 256/1000
0.08 = 8/100
Thus, 0.256/0.08 = (256/1000)/ (8/100)
Now, convert the division into multiplication as explained while solving for fractions.
= (256/1000) × (100/8)
= (256/80)
= 3.2
Therefore, 0.256/0.08 = 3.2
er than 1, the quotient will be a real number between 0 and 1.
| Related Links | |
| Coin Toss Probability Formula | Probability |
| Probability formula | Consecutive Integers Formula |
Division Formula
What is meant by the divide in math?
How do you divide two numbers?
What are the 3 parts of division?
What is n divided by 1?










