Fluid Dynamics Formula - Definition, Examples
Fluid dynamics formula is essential in understanding and designing systems that involve the movement of fluids. It plays a crucial role in various fields.
Murtaza Mushtaq26 Sept, 2023
Share
Definition Of Fluid Dynamics
Fluid dynamics is the study of the motion of fluids, which can be classified into two main categories: liquids and gases. It deals with the behavior of these substances when they are in motion, including how they flow around objects and interact with each other. Fluid dynamics is a fundamental branch of physics and engineering that has numerous real-world applications.1.2 Importance of Fluid Dynamics
Fluid dynamics is essential in understanding and designing systems that involve the movement of fluids. It plays a crucial role in various fields, including aerospace engineering, civil engineering, mechanical engineering, biology, and environmental science. For instance, it helps in designing efficient aircraft, predicting weather patterns, and optimizing the performance of cardiovascular devices.1.3 Types of Fluids
Fluids are substances that can flow and take the shape of their containers. They can be categorized into two main types: - Liquids: Liquids are relatively incompressible and have a definite volume. They flow readily and do not expand to fill their containers. Water, oil, and blood are examples of liquids. - Gases: Gases are highly compressible and can expand to fill their containers. They have no definite shape or volume. Examples of gases include air, helium, and carbon dioxide.Also Check - Energy Level Formula
1.4 Properties of Fluids
Before delving into the equations and principles of fluid dynamics, it's essential to understand some fundamental properties of fluids: - Density (ρ) : Density is the mass per unit volume of a fluid and is typically measured in kilograms per cubic meter (kg/m³). It is denoted by the Greek letter rho (ρ). - Pressure (P) : Pressure is the force per unit area exerted by a fluid on its surroundings. It is measured in pascals (Pa), where 1 Pa is equal to 1 N/m². - Velocity (v): Velocity is the rate of change of position of a fluid element with respect to time. It has both magnitude and direction. - Viscosity (μ): Viscosity is a measure of a fluid's resistance to flow. It determines whether a fluid behaves as a thick, slow-moving liquid (high viscosity) or a thin, fast-moving liquid (low viscosity). - Temperature (T) : Temperature affects the density and viscosity of a fluid. It is typically measured in degrees Celsius (°C) or kelvin (K).Also Check - Ohm's Law Formula
2. Fluid Kinematics
2.1 Description of Fluid Motion Fluid motion can be described in terms of the movement of individual fluid particles or the behavior of fluid elements within a flow field. To analyze fluid motion, we often use concepts such as position, velocity, and acceleration. 2.2 Streamlines, Pathlines, and Streaklines In fluid dynamics, there are three important concepts to describe the motion of fluid particles: - Streamlines: Streamlines are imaginary lines that are tangent to the velocity vector of the fluid at every point. They represent the instantaneous direction of fluid motion. - Pathlines: Pathlines are the actual paths traced by individual fluid particles as they move through the fluid over time. They provide information about the history of fluid motion. - Streaklines: Streaklines are created by releasing a continuous line of fluid particles from a fixed point. They show the spatial distribution of fluid particles at a particular instant.Also Check - Inductance Formula
2.3 Velocity and Acceleration Fields To fully understand fluid motion, we need to consider the velocity and acceleration fields. These fields describe how velocity and acceleration vary at different points within the fluid: - Velocity Field (v): The velocity field represents the velocity vector at each point in the fluid. Mathematically, it can be expressed as v = (u, v, w), where u, v, and w are the components of velocity in the x, y, and z directions, respectively. - Acceleration Field (a): The acceleration field describes how acceleration varies throughout the fluid. It can include components like gravitational acceleration and changes in velocity due to pressure gradients.Also Check - Light Formula
3. Fluid Dynamics Equations
3.1 The Continuity Equation The continuity equation is a fundamental equation in fluid dynamics that expresses the principle of conservation of mass. It states that the mass flow rate into and out of a control volume must be equal: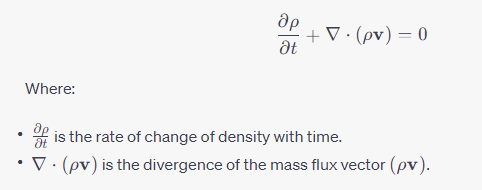
This equation ensures that mass is conserved in a fluid system, meaning that the total mass within a control volume remains constant over time.
3.2 The Navier-Stokes Equations
The Navier-Stokes equations are a set of partial differential equations that govern the motion of fluids. They are essential for describing the behavior of viscous fluids and are derived from the principles of conservation of mass and momentum. The full Navier-Stokes equations consist of three equations, one for each spatial direction (x, y, and z), but we'll focus on the general form for an incompressible fluid:
These equations describe how the velocity field \(\mathbf{v}\) evolves over time under the influence of pressure gradients and viscous forces. Solving the Navier-Stokes equations for a specific problem allows us to predict the flow behavior of a fluid.
3.3 Bernoulli's Equation
Bernoulli's equation is a fundamental equation in fluid dynamics that relates the pressure, velocity, and elevation of a fluid particle in a steady, inviscid flow. It is derived from the conservation of energy for a fluid element moving along a streamline and is expressed as:
Bernoulli's equation is a powerful tool for analyzing fluid flow problems, particularly in situations where the flow can be approximated as inviscid and steady. It is commonly used in applications such as aerodynamics, hydraulics, and the design of fluid transportation systems.
4. Types of Flows
4.1 Steady vs. Unsteady Flows Fluid flows can be categorized into two main types based on their time dependence: - Steady Flow: In steady flow, the velocity and other flow properties at a given point do not change with time. It is as if the flow remains constant over time. Steady flow is often assumed in many engineering applications, especially when simplifying complex problems. - Unsteady Flow: Unsteady flow, on the other hand, involves variations in velocity and other flow properties at a given point over time. It is commonly encountered in transient or dynamic situations, such as when a valve is suddenly opened or closed. 4.2 Incompressible vs. Compressible Flows Another important classification of fluid flows is based on the compressibility of the fluid: - Incompressible Flow: In incompressible flow, the density of the fluid remains nearly constant. This is a valid assumption for liquids and gases at low speeds or when the flow speed is much less than the speed of sound in the fluid. - Compressible Flow: Compressible flow occurs when changes in pressure and velocity significantly affect the density of the fluid. It is commonly observed at high speeds or in gases where the effects of compressibility are significant, such as in supersonic and hypersonic aerodynamics. 4.3 Laminar vs. Turbulent Flows Fluid flows can also be categorized based on the nature of fluid motion within the flow: - Laminar Flow: Laminar flow is characterized by smooth, orderly, and predictable fluid motion. Fluid layers move parallel to each other without significant mixing or turbulence. It is typically associated with low Reynolds numbers and is common in viscous fluids. - Turbulent Flow: Turbulent flow is characterized by chaotic and irregular fluid motion. It involves the formation of eddies, swirls, and vortices, leading to mixing and increased friction. Turbulent flow is associated with high Reynolds numbers and is commonly encountered in fast-moving fluids. 4.4 Viscous vs. Inviscid Flows Viscosity is a property that determines a fluid's resistance to deformation and shear. Based on the viscosity of the fluid, flows can be classified as: - Viscous Flow: In viscous flow, the effects of fluid viscosity are significant, leading to the development of boundary layers and shear stresses at solid surfaces. Viscous flow is common in many practical situations and is described by the Navier-Stokes equations. - Inviscid Flow: In inviscid flow, fluid viscosity is neglected, and the flow is considered frictionless. While this simplification is not always accurate, it is often used in aerodynamics and other applications where the effects of viscosity are negligible.Fluid Dynamics Formula FAQs
What is fluid dynamics?
Fluid dynamics is the study of the behavior of fluids (liquids and gases) in motion. It examines how fluids flow, interact with objects, and the forces that govern their movement.
Why is fluid dynamics important?
Fluid dynamics is crucial for understanding and designing systems involving fluid flow, such as aircraft, pipelines, weather prediction, and medical devices. It helps optimize efficiency, safety, and performance in various fields.
What are the Navier-Stokes equations?
The Navier-Stokes equations are fundamental equations in fluid dynamics that describe how fluids move. They account for factors like pressure, velocity, and viscosity, helping predict fluid behavior.
What's the difference between laminar and turbulent flow?
Laminar flow is smooth and orderly, with fluid layers moving in parallel. Turbulent flow is chaotic and characterized by swirling vortices and mixing, common at high speeds or with high viscosity.
Where is fluid dynamics applied in everyday life?
Fluid dynamics has diverse applications, from designing airplanes and bridges to understanding blood flow in the human body and predicting weather patterns. It touches many aspects of our daily lives and technological advancements.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App