Lagrange Mean Value Theorem Formula: Examples and Solution

The Lagrange Mean Value Theorem is an extension of the Rolle Mean Value Theorem in calculus. This theorem asserts that for a curve between two distinct points, there must exist a point on the curve where the tangent line is parallel to the secant line connecting those two points. Sometimes, the Lagrange Mean Value Theorem is simply referred to as the Mean Value Theorem.

In our study, we will delve deeper into the Lagrange Mean Value Theorem, explore its proof, understand its connection with the Rolle Mean Value Theorem, and illustrate its principles with examples. Additionally, we will address frequently asked questions (FAQs) related to this theorem.

What Is Lagrange Mean Value Theorem?

The Lagrange Mean Value Theorem can be succinctly stated as follows: For any two points on a given curve, there exists a point on that curve where the tangent line is parallel to the secant line connecting those two points.

Statement of Lagrange Mean Value Theorem: Let a function f be defined such that f : [a, b] → R be a continuous function on [a, b] and differentiable on (a, b). Then there exists some a point c in this interval (a, b) such that the derivative of the function at the point c is equal to the difference of the function values at these points, divided by the difference of the point values

This theorem provides a fundamental connection between the behavior of a function and its derivative on a closed interval, highlighting the existence of specific points where the instantaneous rate of change (given by the derivative) matches the average rate of change over that interval.

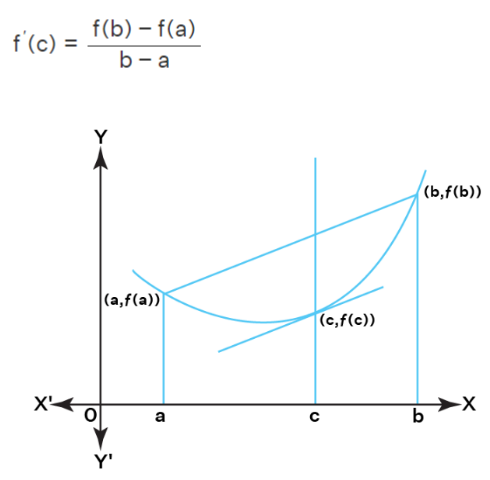
To comprehend the Lagrange Mean Value Theorem geometrically, consider the graph of the equation as y = f(x). Here the graph curve of y = f(x) is passing through the points (a, f(a)), (b, f(b)), and there exists a point (c, f(c)) midway between these points and on the curve. The slope of the secant line passing through these points (a, f(a)), (b, f(b)), is

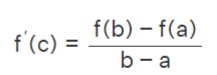
And the slope of the tangent line touching the curve at the point(c, f(c)), is f'(c). Further, the lagrange mean value theorem states that the tangent at a point (c. f(c)) is parallel to the secant line passing through the points (a, f(a)), (b, f(b)), and their slopes are equal. Hence we have

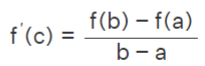
Also Check – Volume of a Cylinder Formula

Proof of Lagrange Mean Value Theorem

Statement: The lagrange mean value theorem states that if a function f is continuous over the closed interval [a,b], and differentiable over the open interval (a,b), then there exists at least one point c in the interval (a,b) such that the slope of the tangent at the point c is equal to the slope of the secant through the endpoints of the curve such that f'(c) =

Also Check – Factors and multiples Formula

Lagrange Mean Value Theorem Formula

Example:

Verify Mean Value Theorem for the function f(x) = x2 – 4x – 3 in the interval [a, b], where a = 1 and b = 4.

Solution:

Given,

f(x) = x2 – 4x – 3

f'(x) = 2x – 4

a = 1 and b = 4 (given)

f(a) = f(1) = (1)2 – 4(1) – 3 = 1 – 4 – 3 = -6

f(b) = f(4) = (4)2 – 4(4) – 3 = -3

Now,

[f(b) – f(a)]/ (b – a) = (-3 + 6)/(4 – 1) = 3/3 = 1

As per the mean value theorem statement, there is a point c ∈ (1, 4) such that f'(c) = [f(b) – f(a)]/ (b – a), i.e. f'(c) = 1.

2c – 4 = 1

2c = 5

c = 5/2 ∈ (1, 4)

Verification: f'(c) = 2(5/2) – 4 = 5 – 4 = 1

Hence, verified the mean value theorem.

Also Check – Rational Number Formula

Lagrange Mean Value Theorem vs Rolle's Mean Value Theorem

While Rolle's theorem specifically deals with situations where the function values at the endpoints are equal, Lagrange's theorem relaxes this condition and focuses on the relationship between the derivative and the average rate of change of the function over the interval.

Both theorems highlight the existence of specific points where the behavior of the function, as expressed by its derivative, relates to the properties of the function over the given interval.