
NCERT Solutions for Class 12 Maths Chapter 1 Excercise 1.4 (Relations and Functions)
NCERT Solutions for Class 12 Maths Chapter 1 Excercise 1.4 Relations and Functions is prepared by academic team of Physics Wallah. We have prepared NCERT Solutions for all exercise of chapter 1. Given below is step by step solutions of all questions given in NCERT textbook for Chapter 1 Relations and Functions.NCERT Solutions for Class 12 Physics
NCERT Solutions for Class 12 Maths Chapter 1 Excercise 1.4 Overview
These crucial subjects are covered in NCERT Solutions Class 12 Maths Chapter 1. To fully grasp the concepts presented in the chapter and make effective use of the provided solutions, students are urged to look over each topic in detail. The teachers at Physics Wallah have been working very hard to help students better understand the concepts that are taught in this chapter, and the result is these solutions. The intention is for students to achieve excellent exam scores with ease after reviewing and practicing these answers.NCERT Solutions for Class 12 Maths Chapter 1 Excercise 1.4 PDF
For NCERT Solutions for Class 12 Maths Chapter 1 Excercise 1.4, our team of teachers at Physics Wallah has created comprehensive solutions to aid students in comprehending and applying chapter themes. These questions aim to facilitate students' understanding of explanations. The NCERT Solutions for Class 12 Maths, Chapter 1 PDF may be downloaded by clicking the following link:NCERT Solutions Class 12 Maths Chapter 1 PDF Download Link
NCERT Solutions for Class 12 Maths Chapter 1 Excercise 1.4
Solve The Following Questions NCERT Solutions for Class 12 Maths Chapter 1 Excercise 1.4
Question 1. Determine whether or not each of the definition of given below gives a binary operation. In the event that * is not a binary operation, give justification for this. (i) On Z + , define * by a * b = a − b (ii) On Z + , define * by a * b = ab (iii) On R, define * by a * b = ab 2 (iv) On Z + , define * by a * b = |a − b| (v) On Z + , define * by a * b = a Solution : (i) On Z + , * is defined by a * b = a − b. It is not a binary operation as the image of (1, 2) under * is 1 * 2 = 1 − 2 = −1 ∉ Z + . (ii) On Z + , * is defined by a * b = ab. It is seen that for each a, b ∈ Z + , there is a unique element ab in Z + . This means that * carries each pair (a, b) to a unique element a * b = ab in Z + . Therefore, * is a binary operation. (iii) On R, * is defined by a * b = ab 2 . It is seen that for each a, b ∈ R, there is a unique element ab 2 in R. This means that * carries each pair (a, b) to a unique element a * b = ab 2 in R. Therefore, * is a binary operation. (iv) On Z + , * is defined by a * b = |a − b|. It is seen that for each a, b ∈ Z + , there is a unique element |a − b| in Z + . This means that * carries each pair (a, b) to a unique element a * b = |a − b| in Z + . Therefore, * is a binary operation. (v) On Z + , * is defined by a * b = a. * carries each pair (a, b) to a unique element a * b = a in Z + . Therefore, * is a binary operation.NCERT Solutions for Class 12 Maths Chapter 1 Exercise 1.1
Question 2. For each binary operation * defined below, determine whether * is commutative or associative:(i) On Z, define a * b = a − b
(ii) On Q, define a * b = ab + 1
(iii) On Q, define a * b =ab/2
(iv) On Z + , define a * b = 2 ab
(v) On Z + , define a * b = a b
(vi) On R − {−1}, define a.b = a/b+1
Solution : (i) On Z , * is defined by a * b = a − b . It can be observed that 1 * 2 = 1 − 2 = 1 and 2 * 1 = 2 − 1 = 1. ∴1 * 2 ≠ 2 * 1; where 1, 2 ∈ Z Hence, the operation * is not commutative. Also we have: (1 * 2) * 3 = (1 − 2) * 3 = −1 * 3 = −1 − 3 = −4 1 * (2 * 3) = 1 * (2 − 3) = 1 * −1 = 1 − (−1) = 2 ∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ Z Hence, the operation * is not associative. (ii) On Q , * is defined by a * b = ab + 1. It is known that: ab = ba &mnForE; a, b ∈ Q ⇒ ab + 1 = ba + 1 &mnForE; a, b ∈ Q ⇒ a * b = a * b &mnForE; a, b ∈ Q Therefore, the operation * is commutative. It can be observed that: (1 * 2) * 3 = (1 × 2 + 1) * 3 = 3 * 3 = 3 × 3 + 1 = 10 1 * (2 * 3) = 1 * (2 × 3 + 1) = 1 * 7 = 1 × 7 + 1 = 8 ∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ Q Therefore, the operation * is not associative. (iii) On Q , * is defined by a * b = ab/2 It is known that: ab = ba &mnForE; a, b ∈ Q ⇒ ab/2 = ba/2 &mn ForE; a, b ∈ Q ⇒ a * b = b * a &mnForE; a, b ∈ Q Therefore, the operation * is commutative. For all a, b , c ∈ Q , we have: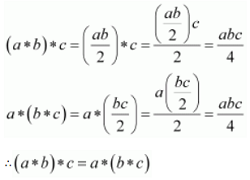 Therefore, the operation * is associative.
(iv) On
Z
+
, * is defined by
a
*
b
= 2
ab
.
It is known that:
ab
=
ba
&mnForE;
a, b
∈
Z
+
⇒ 2
ab
= 2
ba
&mnForE;
a, b
∈
Z
+
⇒
a
*
b
=
b
*
a
&mnForE;
a, b
∈
Z
+
Therefore, the operation * is commutative.
It can be observed that:
Therefore, the operation * is associative.
(iv) On
Z
+
, * is defined by
a
*
b
= 2
ab
.
It is known that:
ab
=
ba
&mnForE;
a, b
∈
Z
+
⇒ 2
ab
= 2
ba
&mnForE;
a, b
∈
Z
+
⇒
a
*
b
=
b
*
a
&mnForE;
a, b
∈
Z
+
Therefore, the operation * is commutative.
It can be observed that:
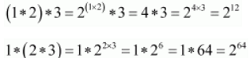 ∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈
Z
+
Therefore, the operation * is not associative.
(v) On
Z
+
, * is defined by
a
*
b
=
a
b
.
It can be observed that:
1 x2 = 1
2
=1 and 2x 1 =2
1
= 2
∴ 1 * 2 ≠ 2 * 1 ; where 1, 2 ∈
Z
+
Therefore, the operation * is not commutative.
It can also be observed that:
∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈
Z
+
Therefore, the operation * is not associative.
(v) On
Z
+
, * is defined by
a
*
b
=
a
b
.
It can be observed that:
1 x2 = 1
2
=1 and 2x 1 =2
1
= 2
∴ 1 * 2 ≠ 2 * 1 ; where 1, 2 ∈
Z
+
Therefore, the operation * is not commutative.
It can also be observed that:
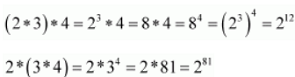 ∴(2 * 3) * 4 ≠ 2 * (3 * 4) ; where 2, 3, 4 ∈
Z
+
Therefore, the operation * is not associative.
(vi) On
R
, * − {−1} is defined by a.b = a/b+1
It can be observed that 1 x 2 = 1/2+1 = 1/2 and 2 x 1 = 2/1+1 = 2/2
∴1 * 2 ≠ 2 * 1 ; where 1, 2 ∈
R
− {−1}
Therefore, the operation * is not commutative.
It can also be observed that:
∴(2 * 3) * 4 ≠ 2 * (3 * 4) ; where 2, 3, 4 ∈
Z
+
Therefore, the operation * is not associative.
(vi) On
R
, * − {−1} is defined by a.b = a/b+1
It can be observed that 1 x 2 = 1/2+1 = 1/2 and 2 x 1 = 2/1+1 = 2/2
∴1 * 2 ≠ 2 * 1 ; where 1, 2 ∈
R
− {−1}
Therefore, the operation * is not commutative.
It can also be observed that:
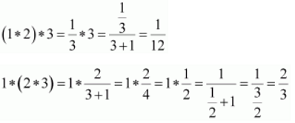 ∴ (1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈
R
− {−1}
Therefore, the operation * is not associative.
∴ (1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈
R
− {−1}
Therefore, the operation * is not associative.
NCERT Solutions for Class 12 Maths Chapter 1 Miscellaneous Exercise
Question 3. Consider the binary operation ∨ on the set {1, 2, 3, 4, 5} defined by a ∨b = min {a, b}. Write the operation table of the operation∨. Solution : The binary operation ∨ on the set {1, 2, 3, 4, 5} is defined as a ∨ b = min {a, b} & mn For E; a, b ∈ {1, 2, 3, 4, 5}. Thus, the operation table for the given operation ∨ can be given as:| ∨ | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 | 2 |
| 3 | 1 | 2 | 3 | 3 | 3 |
| 4 | 1 | 2 | 3 | 4 | 4 |
| 5 | 1 | 2 | 3 | 4 | 5 |
| * | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 1 | 3 | 1 | 1 |
| 4 | 1 | 2 | 1 | 4 | 1 |
| 5 | 1 | 1 | 1 | 1 | 5 |
NCERT Solutions for Class 12 Maths Chapter 1 Exercise 1.3
Question 5. Let*′ be the binary operation on the set {1, 2, 3, 4, 5} defined by a *′ b = H.C.F. of a and b. Is the operation *′ same as the operation * defined in Exercise 4 above? Justify your answer. Solution : The binary operation *′ on the set {1, 2, 3 4, 5} is defined as a *′ b = H.C.F of a and b. The operation table for the operation *′ can be given as:| *′ | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 1 | 3 | 1 | 1 |
| 4 | 1 | 2 | 1 | 4 | 1 |
| 5 | 1 | 1 | 1 | 1 | 5 |
| * | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 2 | 6 | 4 | 10 |
| 3 | 3 | 6 | 3 | 12 | 15 |
| 4 | 4 | 4 | 12 | 4 | 20 |
| 5 | 5 | 10 | 15 | 20 | 5 |
(v) a * b = ab/4 (vi) a * b = ab 2
Find which of the binary operations are commutative and which are associative. Ans.



10. Find which of the operations given above has identity.
Solution : Let the identity be I. Question
11. Let A = N × N and * be the binary operation on A defined by
(a, b) * (c, d) = (a + c, b + d)
Show that * is commutative and associative. Find the identity element for * on A, if any.
Solution :
A = N × N
* is a binary operation on A and is defined by:
(a, b) * (c, d) = (a + c, b + d)
Let (a, b), (c, d) ∈ A
Then, a, b, c, d ∈ N
We have:
(a, b) * (c, d) = (a + c, b + d)
(c, d) * (a, b) = (c + a, d + b) = (a + c, b + d)
[Addition is commutative in the set of natural numbers]
∴(a, b) * (c, d) = (c, d) * (a, b)
Therefore, the operation * is commutative.
Now, let (a, b), (c, d), (e, f) ∈A
Then, a, b, c, d, e, f ∈ N
We have:
Question
11. Let A = N × N and * be the binary operation on A defined by
(a, b) * (c, d) = (a + c, b + d)
Show that * is commutative and associative. Find the identity element for * on A, if any.
Solution :
A = N × N
* is a binary operation on A and is defined by:
(a, b) * (c, d) = (a + c, b + d)
Let (a, b), (c, d) ∈ A
Then, a, b, c, d ∈ N
We have:
(a, b) * (c, d) = (a + c, b + d)
(c, d) * (a, b) = (c + a, d + b) = (a + c, b + d)
[Addition is commutative in the set of natural numbers]
∴(a, b) * (c, d) = (c, d) * (a, b)
Therefore, the operation * is commutative.
Now, let (a, b), (c, d), (e, f) ∈A
Then, a, b, c, d, e, f ∈ N
We have:
 Question
12. State whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation * on a set N,
a
*
a
=
a ∀
a
* N.
(ii) If * is a commutative binary operation on N, then a * (b * c) = (c * b) * a
Solution :
(i) Define an operation * on N as:
a * b = a + b a, b ∈ N
Then, in particular, for b = a = 3, we have:
3 * 3 = 3 + 3 = 6 ≠ 3
Therefore, statement (i) is false.
(ii) R.H.S. = (c * b) * a
= (b * c) * a [* is commutative]
= a * (b * c) [Again, as * is commutative]
= L.H.S.
∴ a * (b * c) = (c * b) * a
Therefore, statement (ii) is true.
Question
13. Consider a binary operation * on N defined as a * b = a
3
+ b
3
. Choose the correct answer.
(A) Is * both associative and commutative?
(B) Is * commutative but not associative?
(C) Is * associative but not commutative?
(D) Is * neither commutative nor associative?
Solution :
On N, the operation * is defined as a * b = a
3
+ b
3
.
For, a, b, ∈ N, we have:
a * b = a
3
+ b
3
= b
3
+ a
3
= b * a [Addition is commutative in N]
Therefore, the operation * is commutative.
It can be observed that:
(1*2)*3 = (1
3
+2
3
)*3 = 9 * 3 = 93 + 33 = 729 + 27 = 756
Also, 1*(2*3) = 1*(2
3
+3
3
) = 1*(8 +27) = 1 × 35
= 1
3
+35
3
= 1 +(35)
3
= 1 + 42875 = 42876.
∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ N
Therefore, the operation * is not associative.
Hence, the operation * is commutative, but not associative. Thus, the correct answer is B.
Question
12. State whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation * on a set N,
a
*
a
=
a ∀
a
* N.
(ii) If * is a commutative binary operation on N, then a * (b * c) = (c * b) * a
Solution :
(i) Define an operation * on N as:
a * b = a + b a, b ∈ N
Then, in particular, for b = a = 3, we have:
3 * 3 = 3 + 3 = 6 ≠ 3
Therefore, statement (i) is false.
(ii) R.H.S. = (c * b) * a
= (b * c) * a [* is commutative]
= a * (b * c) [Again, as * is commutative]
= L.H.S.
∴ a * (b * c) = (c * b) * a
Therefore, statement (ii) is true.
Question
13. Consider a binary operation * on N defined as a * b = a
3
+ b
3
. Choose the correct answer.
(A) Is * both associative and commutative?
(B) Is * commutative but not associative?
(C) Is * associative but not commutative?
(D) Is * neither commutative nor associative?
Solution :
On N, the operation * is defined as a * b = a
3
+ b
3
.
For, a, b, ∈ N, we have:
a * b = a
3
+ b
3
= b
3
+ a
3
= b * a [Addition is commutative in N]
Therefore, the operation * is commutative.
It can be observed that:
(1*2)*3 = (1
3
+2
3
)*3 = 9 * 3 = 93 + 33 = 729 + 27 = 756
Also, 1*(2*3) = 1*(2
3
+3
3
) = 1*(8 +27) = 1 × 35
= 1
3
+35
3
= 1 +(35)
3
= 1 + 42875 = 42876.
∴(1 * 2) * 3 ≠ 1 * (2 * 3) ; where 1, 2, 3 ∈ N
Therefore, the operation * is not associative.
Hence, the operation * is commutative, but not associative. Thus, the correct answer is B.
NCERT Solutions for Class 12 Maths Chapter 1 Excercise 1.4 FAQs
What are the 4 types of relation in math?
How many relations are functions?
What does F of G mean in math?
What is universal relation?
What is a relation called in math?










