NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4 PDF
NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4 has been provided here. Students can refer to these solutions before their examination for better understanding.
Ananya Gupta9 Jan, 2025
Share
NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4: NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4 provide a detailed understanding of the application of trigonometric identities to solve various problems.
These solutions are created to help students develop a strong foundation in trigonometry, enabling them to approach problems systematically. By practicing these solutions students can enhance their problem-solving skills and prepare effectively for their board exams.NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4 Overview
Exercise 8.4 of Chapter 8, Introduction to Trigonometry focuses on applying trigonometric concepts to solve problems involving heights and distances. This exercise emphasizes the use of trigonometric ratios such as sine, cosine, and tangent to calculate unknown heights, distances, or angles.- Angles of Elevation and Depression : Understanding and calculating angles formed when looking up or down at an object.
- Problem-solving : Using trigonometric ratios to find the height of an object, distance between two points, or other related quantities.
- Visual Interpretation : Translating verbal descriptions into diagrams to aid calculations.
CBSE Class 10 Maths Sample Paper 2024-25
NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4 PDF
The NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4 are now available in PDF format, providing step-by-step solutions to all the problems in this exercise. This PDF is designed to help students understand and apply trigonometric concepts effectively, including solving problems involving heights, distances, angles of elevation, and angles of depression. The detailed explanations and solved examples ensure clarity and assist in exam preparation. You can access the PDF from the link provided below to enhance your understanding and practice at your own pace.NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4 PDF
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.4
Below is the NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Exercise 8.4Solve the followings Questions.
1. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.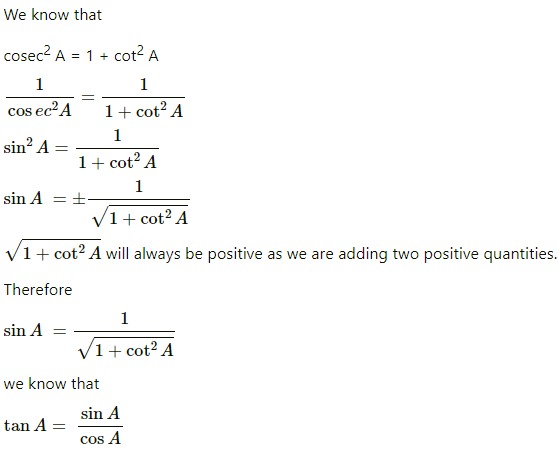
2. Write all the other trigonometric ratios of ∠A in terms of sec A.
Answer:
3. Evaluate :
(i) (sin
2
63° + sin
2
27°)/(cos
2
17° + cos
2
73°)
(ii) sin 25° cos 65° + cos 25° sin 65°
Answer:
(i) (sin 2 63° + sin 2 27°)/(cos 2 17° + cos 2 73°)
(ii) sin 25° cos 65° + cos 25° sin 65°
Choose the correct option. Justify your choice.
4. (i) 9 sec 2 A - 9 tan 2 A = (A) 1 (B) 9 (C) 8 (D) 0 (ii) (1 + tan θ + sec θ) (1 + cot θ - cosec θ) (A) 0 (B) 1 (C) 2 (D) - 1 (iii) (secA + tanA) (1 - sinA) = (A) secA (B) sinA (C) cosecA (D) cosA (iv) 1+tan 2 A/1+cot 2 A = (A) sec 2 A (B) -1 (C) cot 2 A (D) tan 2 AAnswer:
(i) (i) 9 sec 2 A - 9 tan 2 A = (A) 1 (B) 9 (C) 8 (D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ - cosec θ)
(A) 0 (B) 1 (C) 2 (D) - 1
(iii) (secA + tanA) (1 - sinA) =
(A) secA (B) sinA (C) cosecA (D) cosA
(iv) 1+tan
2
A/1+cot
2
A =
(A) sec
2
A (B) -1 (C) cot
2
A (D) tan
2
A
5. Prove the following identities, where the angles involved are acute angles for which the
expressions are defined.
(i) (cosec θ - cot θ)
2
= (1-cos θ)/(1+cos θ)
(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ
[Hint : Write the expression in terms of sin θ and cos θ]
(iv) (1 + sec A)/sec A = sin
2
A/(1-cos A)
[Hint : Simplify LHS and RHS separately]
(v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A,using the identity cosec
2
A = 1+cot
2
A.
(vi) √1 + sin A/1 - sin A = sec A+ tan A
(vii) (sin θ - 2sin
3
θ)/(2cos
3
θ-cos θ) = tan θ
(viii) (sin A + cosec A)
2
+ (cos A + sec A)
2
= 7+tan
2
A+cot
2
A
(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)
[Hint : Simplify LHS and RHS separately]
(x) (1+tan
2
A/1+cot
2
A) = (1-tan A/1-cot A)
2
= tan
2
A
Answer:
(i) (cosec θ - cot θ) 2 = (1-cos θ)/(1+cos θ)
(ii) cos A/(1+sin A) + (1+sin A)/cos A = 2 sec A
(iii) tan θ/(1-cot θ) + cot θ/(1-tan θ) = 1 + sec θ cosec θ
[Hint : Write the expression in terms of sin θ and cos θ]
(iv) (1 + sec A)/sec A = sin
2
A/(1-cos A)
[Hint : Simplify LHS and RHS separately]
(v) (cos A–sin A+1)/(cos A+sin A–1) = cosec A + cot A,using the identity cosec
2
A = 1+cot
2
A
(vi) √1 + sin A/1 - sin A = sec A+ tan A
LHS = 1 + sin A/(1 - sin A) .....(1) Multiplying and dividing by (1 + sin A) ⇒ (1 + sin A)(1 + sin A/1 - sin A)(1 + sin A) = (1 + sin A)²/(1 - sin² A) [a² - b² = (a - b)(a + b)] = (1 + sinA)/1 - sin² A = 1 + sin A/cos² A = 1 + sin A/cos A = 1/cos A + sin A/cos A = sec A + tan A = R.H.S (vii) (sin θ - 2sin 3 θ)/(2cos 3 θ-cos θ) = tan θ
(viii) (sin A + cosec A)
2
+ (cos A + sec A)
2
= 7+tan
2
A+cot
2
A
(ix) (cosec A – sin A)(sec A – cos A) = 1/(tan A+cotA)
[Hint : Simplify LHS and RHS separately]
(x) (1+tan
2
A/1+cot
2
A) = (1-tan A/1-cot A)
2
= tan
2
A
Benefits of Solving NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4
- Conceptual Clarity : By solving the problems in Exercise 8.4, students gain a deeper understanding of trigonometric ratios, particularly in relation to heights and distances. This solidifies their grasp of essential concepts such as angles of elevation and depression, helping them apply these concepts accurately in different scenarios.
- Improved Problem-Solving Skills : The exercise provides a range of problems that require logical thinking and application of trigonometric formulas. By practicing these, students develop problem-solving skills and learn to approach mathematical challenges methodically.
- Boosts Confidence : As students work through the problems and understand the step-by-step solutions, they build confidence in their ability to tackle similar questions in exams, reducing exam anxiety.
- Helps in Exam Preparation : The NCERT solutions for Exercise 8.4 are structured to match the exam pattern. Solving these problems regularly helps students familiarize themselves with the type of questions that might appear in board exams, making them well-prepared for their exams.
- Better Time Management : By practicing with these solutions, students learn to solve problems within a given time frame, which is a crucial skill during exams. This helps them manage time effectively and solve questions efficiently.
- Comprehensive Understanding : The step-by-step solutions in the NCERT PDF make it easier to grasp the process of solving trigonometric problems, ensuring a thorough understanding of the topic and its applications.
- Revision Aid : These solutions are a great resource for revision, allowing students to quickly refresh their memory of important formulas, concepts, and methods before exams.
NCERT Solutions for Class 10 Maths Chapter 8 Exercise 8.4 FAQs
What is Trigonometry?
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of a triangle, particularly right-angled triangles. It is used to find missing angles or sides in a triangle using trigonometric ratios like sine, cosine, and tangent.
What is a right-angled triangle?
A right-angled triangle is a triangle where one of the angles is 90°, and the other two angles are acute. The side opposite the right angle is called the hypotenuse, while the other two sides are referred to as the opposite and adjacent sides.
Why is trigonometry important?
Trigonometry is important because it helps in solving problems related to angles and distances. It has applications in various fields like engineering, physics, astronomy, architecture, and navigation.
What are the trigonometric identities?
Trigonometric identities are equations involving trigonometric functions that are true for all values of the involved angles. Some common identities include:
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.