NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1 PDF
NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1 has been provided here. Students can refer to these solutions before their examination for better understanding.
Ananya Gupta13 Jan, 2025
Share
NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1: NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry Exercise 9.1 focuses on applying trigonometric concepts. This exercise introduces students to practical uses of trigonometry, particularly in situations involving heights and distances.
By using trigonometric ratios such as sine, cosine, and tangent, students learn how to calculate unknown distances or angles in right-angled triangles. The problems in this exercise involve scenarios like finding the height of a building or the distance between two points, making it an essential exercise to enhance problem-solving skills in trigonometry.CBSE Class 10 Previous Year Question Papers
NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1 Overview
Exercise 9.1 of Chapter 9: Some Applications of Trigonometry introduces students to the practical application of trigonometric concepts in real-life situations. The focus of this exercise is on calculating heights, distances, and angles, using trigonometric ratios like sine, cosine, and tangent in right-angled triangles.CBSE Class 10 Maths Sample Paper 2024-25
The problems in this exercise involve scenarios such as finding the height of an object, the distance between two points, or the angle of elevation and depression. These applications help students understand how trigonometry is used to solve practical problems involving angles and distances that cannot be measured directly.Key aspects of the exercise include:
- Angle of Elevation : The angle formed when an observer looks upwards at an object.
- Angle of Depression : The angle formed when an observer looks downwards at an object.
- Trigonometric Ratios : Applying sine, cosine, and tangent to find unknown values in right-angled triangles.
- Problem-Solving : Translating the word problems into mathematical equations using trigonometric ratios and solving them step by step.
NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1 PDF
The NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1 PDF is now available for download. By referring to this PDF students can enhance their understanding of trigonometric concepts and improve their problem-solving skills. The clear explanations and examples help in better grasping the techniques needed to solve these types of problems. You can access the PDF from the link provided below for easy reference and practice.NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1 PDF
Solve the followings Questions.
1. A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see figure ).Answer:
Let AB be the vertical pole Ac be 20 m long rope tied to point C.
In right ΔABC,
sin 30° = AB/AC
⇒ 1/2 = AB/20
⇒ AB = 20/2
⇒ AB = 10
The height of the pole is 10 m.
2. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Answer:
Let AC be the broken part of the tree.
∴ Total height of the tree = AB+AC
In right ΔABC,
cos 30° = BC/AC
⇒ √3/2 = 8/AC
⇒ AC = 16/√3
Also,
tan 30° = AB/BC
⇒ 1/√3 = AB/8
⇒ AB = 8/√3
Total height of the tree = AB+AC = 16/√3 + 8/√3 = 24/√3
3. A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Answer:
There are two slides of height 1.5 m and 3 m. (Given)
Let AB is 1.5 m and PQ be 3 m slides.
ABC is the slide inclined at 30° with length AC and PQR is the slide inclined at
60° with length PR.
A/q,
In right ΔABC,
sin 30° = AB/AC
⇒ 1/2 = 1.5/AC
⇒ AC = 3m
also,
In right ΔPQR,
sin 60° = PQ/PR
⇒ √3/2 = 3/PR
⇒ PR = 2√3 m
Hence, length of the slides are 3 m and 2√3 m respectively.
4. The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Answer:
Let AB be the height of the tower and C is the point elevation which is 30 m away from the foot of the tower.
In right ΔABC,
tan 30° = AB/BC
⇒ 1/√3 = AB/30
⇒ AB = 10√3
Thus, the height of the tower is 10√3 m.
5. A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Answer:
Let BC be the height of the kite from the ground,
AC be the inclined length of the string from the ground and A is the point where string of the kite is tied.
A/q,
In right ΔABC,
sin 60° = BC/AC
⇒ √3/2 = 60/AC
⇒ AC = 40√3 m
Thus, the length of the string from the ground is 40√3 m.
6. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Answer:
Let the boy initially standing at point Y with inclination 30° and then he approaches the building to
the point X with inclination 60°.
∴ XY is the distance he walked towards the building.
also, XY = CD.
Height of the building = AZ = 30 m
AB = AZ - BZ = (30 - 1.5) = 28.5 m
A/q,
In right ΔABD,
tan 30° = AB/BD
⇒ 1/√3 = 28.5/BD
⇒ BD = 28.5√3 m
also,
In right ΔABC,
tan 60° = AB/BC
⇒ √3 = 28.5/BC
⇒ BC = 28.5/√3 = 28.5√3/3 m
∴ XY = CD = BD - BC = (28.5√3 - 28.5√3/3) = 28.5√3(1-1/3) = 28.5√3 × 2/3 = 57/√3 m.
Thus, the distance boy walked towards the building is 57/√3 m.
7. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Answer:
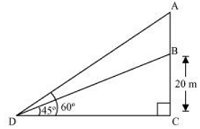Let BC be the 20 m high building.
D is the point on the ground from where the elevation is taken.
Height of transmission tower = AB = AC - BC
In right ΔBCD,
tan 45° = BC/CD
⇒ 1 = 20/CD
⇒ CD = 20 m
also,
In right ΔACD,
tan 60° = AC/CD
⇒ √3 = AC/20
⇒ AC = 20√3 m
Height of transmission tower = AB = AC - BC = (20√3 - 20) m = 20(√3 - 1) m.
8. A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Answer:
Let AB be the height of statue.
D is the point on the ground from where the elevation is taken.
Height of pedestal = BC = AC - AB
In right ΔBCD,
tan 45° = BC/CD
⇒ 1 = BC/CD
⇒ BC = CD.
also,
In right ΔACD,
tan 60° = AC/CD
⇒ √3 = AB+BC/CD
⇒ √3CD = 1.6 m + BC
⇒ √3BC = 1.6 m + BC
⇒ √3BC - BC = 1.6 m
⇒ BC(√3-1) = 1.6 m
⇒ BC = 1.6/(√3-1) m
⇒ BC = 0.8(√3+1) m
Thus, the height of the pedestal is 0.8(√3+1) m.
9. The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Answer:
Let AB be the building and CD be the tower
In ΔCDB,
CB/BD = tan 60º
50/BD = √3
BD = √3/50
In ΔABD,
(AB)/(BD) = tan 30º
AB = 50/√3 x 1/√3 = 50/3 = 16 2/3
Therefore, the height of the building is 16 2/3 m.
10. Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
Answer:
In right triangle PRQ,
Let AB and CD be the poles and O is the point from where the elevation angles are measured.
In ΔABO
(AB)/(BO) = tan 60º
AB/BO = √3
BO = AB/√3
In ΔCDO,
(CD)/(DO) = tan 30º
CD/80 - BO = 1/√3
CD x √3 = 80 - BO
CD x √3 = 80 - AB/√3
CD x √3 + AB/√3 = 80
Since the poles are of equal heights,
CD = AB
CD[√3 + 1/√3] = 80
CD[3+1/√3] = 80
CD = 20√3
BO = AB/√3 = CD/√3 = [20√3/√3]m = 20m
DO = BD − BO = (80 − 20) m = 60 m
Hence the heights of the poles are 20√3 m each and the distances of the point from poles are 20 m and 60 m respectively.
11. A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see figure). Find the height of the tower and the width of the canal.
Answer:
In ΔABC, AB/BC = tan 60º AB/BC = √3 BC = AB/ √3 In ΔABD, AB/BD = tan 30º AB/BC+CD = 1/√3 [AB/(AB/√3) + 20] = 1/√3 [AB x √3/AB + 20 x √3] = 1/√3 3AB = AB + 20√3 = 2AB = 20√3 AB = 10√3m BC = AB/√3 = {10√3/√3}m = 10m Hence height of the tower is 10√3 m and the width of the canal is 10 m. 12. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.Answer:
Let AB be a building and CD be a cable tower.
In ΔABD,
AB/BD = tan 45º
7/BD = 1
BD = 7 m
In ΔACE,
AE = BD = 7 m
CE/AE = tan 60º
CE/7 = √3
CE = 7 x √3
CD = CE + ED = [7 x √3 + 7]m = 7[√3 + 1]m
Hence height of the tower is 7[√3 + 1]m.
13. As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Answer:
Let AB be the lighthouse and the two ships be at point C and D respectively.
In ΔABC,
AB/BC = tan 45º
75/BC = 1
BC = 75 m
In ΔABD,
AB/BD = tan 30º
75/BC+CD = 1/√3
75/75+CD = 1/√3
75 x √3 = 75 + CD
75[√3 - 1]m = CD
Hence the distance between the two ships is 75[√3 - 1]m
14. A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance travelled by the balloon during the interval.
Answer:
In right triangle ABC,
Let the initial position A of balloon change to B after some time and CD be the girl.
In ΔACE,
AE/CE = tan 60º
(AF - EF)/(CE) = tan 60º
88.2 - 1.2/CE = √3
87/CE = √3
CE = 87/√3 = 87x√3m
In ΔBCG,
(BG)/(CG) = tan 30º
88.2 - 1.2/CG = 1/√3
87/CG = 1/√3
CG = 87x√3 m
Distance travelled by balloon = EG = CG − CE
= (87x√3 - 29x√3 )m
= 58√3m
Hence the distance travelled by the balloon during the interval is 58√3 m.
15. A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Answer:
Let AB be the tower.
Initial position of the car is C, which changes to D after six seconds.
In ΔADB,
AB/DB = tan 60º
AB/DB = √3
DB = AB/√3
In ΔABC,
AB/BC = tan 30º
AB/BD + DC = 1/√3
AB √3 = BD + DC
AB √3 = AB/√3 + DC
DC = AB √3 - AB/√3 = AB(√3 - 1/√3) = 2AB/√3
Time taken by the car to travel a distance DC (i.e.2AB/√3) = 6 seconds.
Time taken by the car to travel a distance DB (i.e. AB/√3) = [6/2AB/√3] x [AB/√3] = 6/2 = 3 seconds.
Hence, the further time taken by the car to reach the foot of the tower is 3 seconds.
16. The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Answer:
.png)
Let AQ be the tower and R, S are the points 4m, 9m away from the base of the tower respectively.
The angles are complementary. Therefore, if one angle is θ, the other will be 90 − θ.
In ΔAQR,
AQ/QR = tanΘ
AQ/4 = tanΘ ... 1
In ΔAQS,
AQ/SQ = tan(90 - Θ)
AQ/9 = cot Θ ...2
On multiplying equations (1) & (2)
(AQ/4)(AQ/9) = (tanΘ).(cot Θ)
AQ²/36 = 1
AQ² = 36
AQ = √36
AQ = ±6
However, height cannot be negative.
Therefore, the height of the tower is 6 m
Benefits of Solving NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1
- Strengthening Problem-Solving Skills : The exercise provide a variety of problems that require students to apply trigonometric formulas and methods. This strengthens their analytical and problem-solving abilities, which are essential for exams.
- Better Exam Preparation : Solving the problems in Exercise 9.1 helps students familiarize themselves with the types of questions that could appear in board exams. Regular practice ensures that they are well-prepared for the exam and boosts their confidence.
- Clear Explanation of Solutions : The step-by-step solutions in the NCERT materials provide a clear understanding of how to approach each problem. Students can learn the correct methods for solving trigonometric problems and apply them independently.
- Time Management : By regularly practicing with this exercise, students learn to solve problems within a set time frame, which is important for managing time effectively during exams.
- Foundation for Advanced Topics : This exercise lays the groundwork for more advanced applications of trigonometry in higher classes. Mastery of these basic concepts makes it easier to understand more complex trigonometric concepts in future lessons.
NCERT Solutions for Class 10 Maths Chapter 9 Exercise 9.1 FAQs
What is the focus of Exercise 9.1 in Chapter 9 of Class 10 Maths?
Exercise 9.1 focuses on the practical applications of trigonometry, especially in problems involving heights, distances, and angles of elevation and depression.
How do trigonometric ratios help in solving problems in Exercise 9.1?
Trigonometric ratios help by relating the angles of a right-angled triangle to the lengths of its sides.
What types of problems are included in Exercise 9.1?
The problems in Exercise 9.1 involve practical situations where you need to find the height of objects (such as buildings or trees), the distance between two points, or the angle of elevation/depression in right-angled triangles.
How can NCERT Solutions help in understanding Exercise 9.1?
NCERT Solutions for Exercise 9.1 provide step-by-step explanations and solutions, which help students understand how to apply trigonometric ratios to solve problems.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!
Check out these Related Articles
Join 15 Million students on the app today!
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.