
Quotient Rule Formula: The quotient rule in calculus is utilized to compute the derivative of a function that is expressed as the ratio or division of two differentiable functions. This rule is applicable when determining the derivative of a function written in the form f(x)/g(x), where both f(x) and g(x) are differentiable, and g(x) is not equal to zero. Derived from the product rule and the fundamental concept of derivative limits, the quotient rule is crucial in differentiation.
What is the Quotient Rule in calculus
The Quotient Rule is a method used to compute the derivative of a function presented as a quotient resulting from the division of two differentiable functions. In simple terms, this rule specifies that the derivative of a quotient is determined by the ratio of the numerator's derivative multiplied by the denominator, subtracting the product of the numerator and the derivative of the denominator, all divided by the square of the denominator. This means that if we have a function in the form f(x) = u(x)/v(x), we can determine its derivative using the Quotient Rule expressed as:
f'(x) = [u(x)/v(x)]' = [v(x) × u'(x) - u(x) × v'(x)] / [v(x)] 2
Quotient Rule Formula
Formula for the Quotient Rule The derivative of a quotient of two functions can be computed using the quotient rule derivative formula. This formula is represented as:
f'(x) = [u(x)/v(x)]' = [v(x) × u'(x) - u(x) × v'(x)] / [v(x)] 2
Where,
- f(x) = The function in the form of u(x)/v(x) for which the derivative is being determined.
- u(x) = A differentiable function representing the numerator of the function f(x).
- u ′ (x) = Derivative of function u(x).
- v(x) = A differentiable function representing the denominator of the given function f(x).
- v ′ (x) = Derivative of the function v(x).
Deriving the Quotient Rule Formula
In the earlier section, we familiarized ourselves with the formula for obtaining derivatives of the quotient of two differentiable functions. Now, let's explore the derivation of the quotient rule formula. The proof for the quotient rule formula can be accomplished through various methods, including:
- Utilizing derivative and limit properties
- using implicit differentiation
- Application of the chain rule
Quotient Rule Formula Proof Using Derivative and Limit Properties
Demonstration of Quotient Rule Formula via Derivative and Limit Properties To establish the quotient rule formula utilizing the derivative definition or limits, consider the function f(x)=u(x)/v(x).
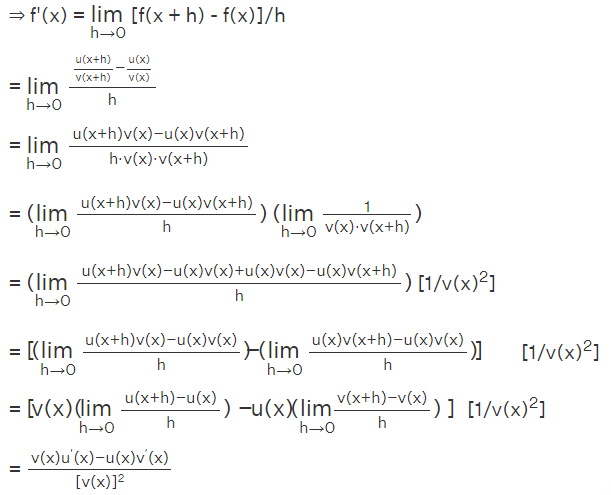
Quotient Rule Formula Proof Using Implicit Differentiation
Demonstration of Quotient Rule Formula Using Implicit Differentiation To establish the quotient rule formula via implicit differentiation, consider a differentiable function f(x)=u(x)/v(x), where u(x)=f(x)⋅v(x).
Applying the product rule, we get u ′ (x)=f ′ (x)⋅v(x)+f(x)⋅v ′ (x). Solving for f ′ (x), we obtain:
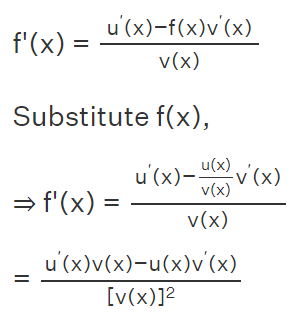
Quotient Rule Formula Proof Using Chain Rule
Proof of Quotient Rule Formula Utilizing Chain Rule The derivation of the quotient rule formula in calculus involves using the chain rule formula. Suppose f(x) is a differentiable function, such that f(x)=u(x)/v(x).
f(x)=u(x)v −1 (x)
Using the product rule,
f ′ (x)=u ′ (x)v −1 (x)+u(x)⋅( d /dx (v −1 (x)))
Applying the power rule to compute the derivative in the second term, we obtain:
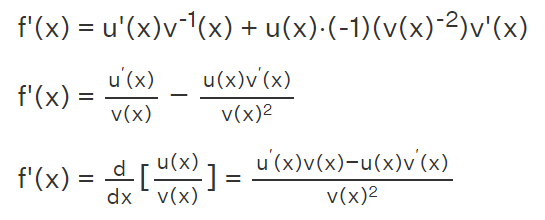
How to Utilize the Quotient Rule for Differentiation
To determine the derivative of a function in the form f(x)=u(x)/v(x), it's essential for both u(x) and v(x) to be differentiable functions.
Follow these steps to find the derivative of a differentiable function f(x)=u(x)/v(x) using the quotient rule:
Step 1: Record the values of u(x) and v(x).
Step 2: Calculate the values of u ′ (x) and v ′ (x), then apply the quotient rule formula, given as:
f'(x) = [u(x)/v(x)]' = [v(x) × u'(x) - u(x) × v'(x)] / [v(x)] 2
Let's examine the following example provided below to gain a clearer understanding of the quotient rule.
Quotient Rule Formula Solved Example
Example: Find f ′ (x) for the function f(x)= 3x/ x 2 +2 using the quotient rule. Solution: Given, f(x)= 3x/ x 2 +2
Where: u(x)=3x
v(x)=(x 2 +2)
u ′ (x)=3
v ′ (x)=2x
Applying the quotient rule: f ′ (x)= [v(x)u ′ (x)−u(x)v ′ (x)] / [v(x)] 2
f ′ (x)=[ (x 2 +2)⋅3−3x⋅2x] / (x 2 +2) 2
f ′ (x) = [3x 2 +6−6x 2 ] / (x 2 +2) 2
f ′ (x)= −3x 2 +6 / (x 2 +2) 2
Answer: The derivative of Answer: The derivative of 3x/x 2 +2 is −3x 2 +6 / (x 2 +2) 2 .
| Related Links | |
| U Substitution Formula | Vertex Formula |
| Foil Formula | Function Notation Formula |
Quotient Rule Formula FAQs
What is the quotient rule in calculus?
What is the quotient rule formula?
How is the quotient rule used in differentiation?
Can the quotient rule be used for any function?










