U Substitution Formula, Definition, Solved Examples
Manoj Kumar3 Nov, 2023
Share
U Substitution Formula: The technique known as U-substitution, or integration by substitution in calculus, provides a method for solving integrals. It stands as a crucial method in mathematics due to its relation to the fundamental theorem of calculus, which is typically used for finding antiderivatives. The U-substitution formula aligns with the chain rule of differentiation, presenting an alternative method akin to the process of differentiation. This formula involves replacing the given function with 'u', integrating 'u' according to the fundamental integration formula, and ultimately substituting the original function back in place of 'u'.
U Substitution Formula
The U-substitution formula involves the replacement of the primary function with 'u'. Hence, the variable 'u' is integrated using the fundamental integration formula. Following integration, the original function is reintroduced in place of 'u'. The formula for U substitution can be expressed as:
∫ f ( g ( x ) ) g ′ ( x ) d x = ∫ f ( u ) d u
where, u = g(x) du = g ′ ( x ) d x
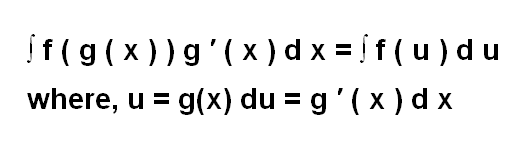
U Substitution Formula Solved Examples
Example 1: Integrate ∫3x(x 2 +4) 4 dx
Solution: Let u=x 2 +4. Then, du=2xdx. Substitute the value of u and du into the integral ∫3x(x 2 +4) 4 dx Using the U-substitution formula: ∫3x(x 2 +4) 4 dx= 3/2 ∫u 4 du This integrates to 3/10 u 5 +c= 3/10(x 2 +4) 5 +c Answer: 3/10(x 2 +4) 5 +c 3/10 u 5 +c= 3/10(x 2 +4) 5 +c Answer: 3/10(x 2 +4) 5 +cExample 2: Integrate ∫ ( 2 − x ) 8 d x
Solution: Let u = (2 - x) So that, du = (-1)dx. Substitute the value of u and du in ∫ ( 2 − x ) 8 d x , replacing all forms of x, getting Using U substitution formula, ∫ ( 2 − x ) 8 d x = ∫ u 8 ( − 1 ) d u = - ∫ u 8 d u = - u 9 / 9 + c = - ( 2 − x ) 9 / 9 + c Answer: - ( 2 − x ) 9 / 9 + cExample 3: Integrate ∫ ( 2 − x ) 10 d x
Solution: Let u = (2 - x) So that, du = (-1)dx. Substitute the value of u and du in ∫ ( 2 − x ) 10 d x , replacing all forms of x, getting Using U substitution formula, ∫ ( 2 − x ) 10 d x = ∫ u 10 ( − 1 ) d u = - ∫ u 10 d u = - u 10 / 10 + c = - ( 2 − x ) 10 / 10 + c Answer: - ( 2 − x ) 10 / 10 + cExample 4: Integrate ∫3x(x 2 +4) 3 dx
Solution: Let u=x 2 +2. Then, du=2xdx. Substitute the value of u and du into the integral ∫3x(x 2 +2) 3 dx Using the U-substitution formula: ∫3x(x 2 +2) 3 dx= 3/2 ∫u 3 du This integrates to 3/8 u 4 +c= 3/8(x 2 +2) 4 +c Answer: 3/8(x 2 +2) 4 +c 3/8 u 4 +c= 3/8(x 2 +2) 4 +c Answer: 3/8(x 2 +2) 4 +cExample 5: Integrate ∫ ( 1 − x ) 5 d x
Solution: Let u = (1 - x) So that, du = (-1)dx. Substitute the value of u and du in ∫ ( 1 − x ) 5 d x , replacing all forms of x, getting Using U substitution formula, ∫ ( 1 − x ) 5 d x = ∫ u 5 ( − 1 ) d u = - ∫ u 5 d u = - u 6 / 6 + c = - ( 1 − x ) 6 / 6 + c Answer: - ( 1 − x ) 6 / 6 + cThese examples demonstrate the application of the U-substitution method to solve integrals, showing how choosing appropriate u and performing necessary manipulations allows for the simplification and solution of the given integrals.
The U-substitution method in calculus is a powerful technique used to solve integrals. Its significance lies in its connection to the fundamental theorem of calculus and its similarity to the chain rule of differentiation. By replacing a given function with 'u', integrating 'u' according to the fundamental integration formula, and then substituting the original function back in place of 'u', this method provides an effective way to simplify and solve integrals.
Explore Now Online Course of Class 9 Neev Fastrack 2024 and Class 10 Udaan Fastrack 2024 to enhance your Maths knowledge. and build a strong foundation.| Related Links | |
| Function Notation Formula | Hexagonal Pyramid Formula |
| Hypothesis Testing Formula | Interquartile Range Formula |
U Substitution Formula FAQs
What is the U Substitution method in calculus?
How does U Substitution work?
What is the fundamental principle of U Substitution?
How do you choose 'u' in U Substitution?
What is the formula for U Substitution?
Live & recorded classes available at easeDashboard for progress trackingMillions of practice questions at your fingertips
