RS Aggarwal Solutions for Class 8 Maths Chapter 1 Exercise 1.3:
The Physics Wallah academic team has produced a comprehensive answer for Chapter 1: Rational Numbers in the RS Aggarwal class 8 textbook. The RS Aggarwal class 8 solution for chapter-1 Rational Numbers Exercise-1C is uploaded for reference only; do not copy the solutions. Before going through the solution of chapter-1 Rational Numbers Exercise-1C, one must have a clear understanding of the chapter-1 Rational Numbers.
Read the theory of chapter-1 Rational Numbers and then try to solve all numerical of exercise-1C. Read the NCERT maths textbook and use the NCERT class 8 maths solutions to answer the exercise's questions if you want to become an expert in the subject. Experts in Physics Wallah have compiled all of the NCERT Solutions.
RS Aggarwal Solutions for Class 8 Maths Chapter 1 Exercise 1.3 Rational Numbers Overview
Chapter 1, Exercise 1.3 of RS Aggarwal’s Class 8 Maths book focuses on Rational Numbers. Rational numbers are those numbers that can be expressed as the ratio of two integers, where the denominator is not zero. This exercise helps students understand and practice the basic operations and properties of rational numbers, such as addition, subtraction, multiplication, and division.
The problems in this exercise involve simplifying rational numbers, finding equivalent forms, and performing arithmetic operations with them. Students learn to handle positive and negative rational numbers and work with different forms of fractions. By solving these problems, students gain a clear understanding of how rational numbers behave under various mathematical operations, reinforcing their foundational skills in algebra and number theory.
The exercise emphasizes the importance of consistency in handling fractions and helps in developing problem-solving strategies for more complex mathematical concepts. Overall, this exercise is crucial for building a strong foundation in working with rational numbers.
What are Rational Numbers?
Rational numbers are those that may be stated as a ratio between two integers in the number system. If the rational number is an integer, it can also be the quotient of the ratio. A non-zero integer q must exist if the rational number is represented by the ratio p/q.
Every integer is a rational number because the denominator can be 1. Class 8 covers all the ideas related to rational numbers; the arithmetic operations and features of rational numbers are presented in detail.
RS Aggarwal Solutions for Class 8 Maths Chapter 1 Exercise 1.3 PDF
Below we have provided RS Aggarwal Solutions for Class 8 Maths Chapter 1 Exercise 1.3 Rational Numbers in detail. This chapter will help you to clear all your doubts regarding the chapter. Students are advised to prepare from these RS Aggarwal Solutions for Class 8 Maths Chapter 1 Exercise 1.3 Rational Numbers before the examinations to perform better.
RS Aggarwal Solutions for Class 8 Maths Chapter 1 Exercise 1.3 PDF
RS Aggarwal Solutions for Class 8 Maths Chapter 1 Exercise 1.3
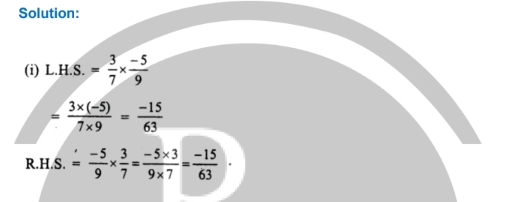
Below we have provided RS Aggarwal Solutions for Class 8 Maths Chapter 1 Exercise 1.3 Rational Numbers –
Question 1.
Solve the following -
Question 2
Verify the Following -
Question 3.
Verify the following -
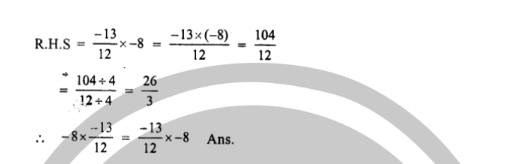
Question 4.
Solve the Following -
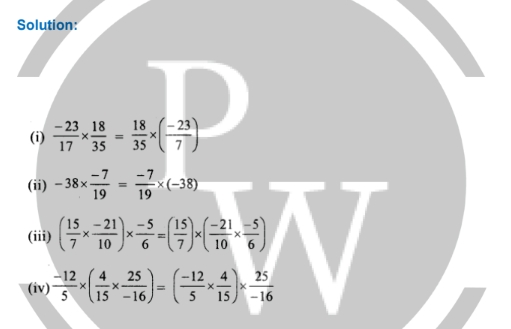
Question 5.
Write the multiplicative inverse of the following -
Question 6.
Find the value of -
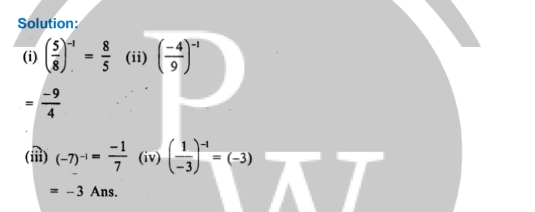
Question 7.
Solve the following equations -
Question 8.
Using appropriate laws, solve -
Benefits of RS Aggarwal Solutions for Class 8 Maths Chapter 1 Exercise 1.3
The RS Aggarwal Solutions for Class 8 Maths Chapter 1 Exercise 1.3 on Rational Numbers offers several benefits:
Concept Clarity
: The solutions provide clear and step-by-step explanations of problems involving rational numbers, helping students understand the concepts of fractions, ratios, and the basic operations involving them.
Practice Opportunities
: The exercise includes a variety of problems that reinforce the understanding of rational numbers, allowing students to practice different scenarios and operations such as addition, subtraction, multiplication, and division.
Problem-Solving Skills
: By working through the solutions, students develop their problem-solving skills and learn to approach and solve mathematical problems systematically.
Foundation Building
: Mastery of this exercise lays a strong foundation for more advanced topics in mathematics, such as algebra and real numbers, ensuring students are well-prepared for future concepts.
Error Correction
: The solutions help identify common mistakes and misunderstandings, guiding students to correct errors and improve their accuracy in handling rational numbers.
Confidence Boost
: As students successfully solve problems and understand the rationale behind each step, their confidence in handling rational numbers and similar mathematical concepts grows.
