ICSE Worksheet for Chapter - 1 Sets Class 8

ICSE Worksheet for Chapter - 1 Sets Class 8

Worksheets For class 8

Summary

Roster Method

In this method a set is described by listing elements separated by commas within braces { }.

Set Builder Method

In this method a set is described by characterizing property P(x) of its element x.

• Cardinal number of a Finite Set
• Operation on Set

1. UNION OF SETS

Let A and B be the sets .The union of A and B is the set of all those elements which belong to A or to B or both A and B.

U B={x: x € A or x € B}.

2. INTERSECTION OF SETS

A ∩ B={x:x € A and x € B}

3. COMPLEMENT OF A SET

A’ ={x € U: x ∉A }

4. DISTRIBUTIVE LAWS

• A U (B ∩C)=(AUB)∩ (AUC)
• A ∩ (B UC)=(A ∩ B)U(A ∩ C)

Subjective

Q1. Let A and B be sets If A ∩ X =B ∩ X= φ and A U X = B UX for some set X, Prove that A=B

Q2. Using properties of sets show that for any two sets A and B ( A U B) ∩ (A ∩ B’) = A

Q3. In a group of 800 people 450 can speak Hindi and 450 can speak English. How many can speak both Hindi and English?

Q4 . There are 40 students in a chemistry class and 60 students in physics class. Find the number of students which are either in physics class or chemistry class in the following cases

(i)The two classes met at the same hour

(ii) The two classes meet at different hours and 20 students are enrolled in both subjects.

1. A =B
2. A10
3. 4
4. 80

Objective

Q1. If A={x € N| x ² ≤ 36} then A is equal to

1. {1,2,3,4,5,6}
2. {6}
3. {0,1,2,3,4,5,6}
4. {-6,-5,… -1,0,1,2,…6}

Q2. The number of subsets of an empty set is

1. 0
2. 1
3. 2
4. 3

Q3. A –B is equal to

1. A ∩ B
2. A ∩ B’
3. A’∩ B’
4. A’ U B’

Q4. If U={1,2,3,4,5,6,7}, A={1,2,3,4,5} B={1,3,5,7} then A’ –B’ is equal to

1. {1, 3, 5}
2. {4,6}
3. {3,4,6}
4. {7}

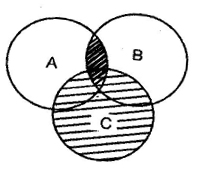
Q5. The shaded region in the Venn’s diagram given below represents

1. (A U B) ∩ C
2. (A ∩ B) U C
3. (A U B) UC
4. (A∩ B ) ∩ C

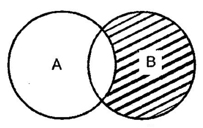
Q6. The shaded region in Venn’s diagram given below represents

1. A –B
2. B- A
3. A’ – B
4. A –B’

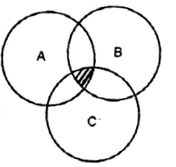
Q7. The shaded region in Venn’s diagram given below represents

1. A∩ B ∩ C
2. A U B ∩ C
3. A U B U C
4. None of these

Q8. Which one of the following is true

1. A U φ= A
2. A U φ =φ
3. A U A =φ
4. A U φ=U

Q9. The set of all those elements of A and B which are common to both is called

1. Union of two sets
2. Intersection of two sets
3. Disjoint sets
4. None of these

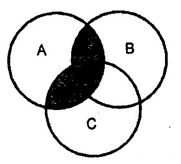
Q10. 3 sets A, B, C are represented by 3 circles in the given Venn diagram. What does the shaded region represents?

1. (A U B) ∩ C
2. A U (B ∩ C)
3. (A∩ B) U C
4. A ∩ (B U C)

Q11. If A be a finite set having n elements and P(A) is its power set, then total number of subsets of P (P(A)) is

1. 2 ⁿ
2. 4 ⁿ
3. 2 ^{(2n )}
4. 2 ²ⁿ

Q12. In a survey of 25 student it was found that 15 had taken maths 12 had taken physics and 11 had taken chemistry 5 had taken math’s and chemistry, 9 had taken maths and physics , 4 had taken physics and chemistry and 3 had taken all the three subjects.

Q13. Let n (U) = 700, n (A) = 200, n (B) = 300 and n(A ∩ B) =100 then (A’ ∩ B’) =

1. 400
2. 600
3. 300
4. 200

Q14. In a class of 55 students the number of students studying different subjects are 23 in maths and 24 in physics, 19 in chemistry, 12 in maths and physics, 9 in maths and chemistry, 7 in physics and chemistry and 4 in all the three subjects. The number of students who have taken exactly one subjects is

1. 20
2. 21
3. 23
4. 22

Q15. Out of 800 boys in a school 224 played cricket, 240 played hockey and 336 played basketball. Out of the total 64 played both basketball and hockey,80 played cricket and basketball and 40 played cricket and hockey, 24 player all the three game The number of boys who did not play any game is

1. 128
2. 216
3. 240
4. 160

Solutions

Objective

1. 1
2. 2
3. 3
4. 4
5. 2
6. 2
7. 1
8. 1
9. 2
10. 4
11. 3
12. 4
13. 3
14. 4
15. 4

Subjective

Q3. 100

For other ICSE Worksheet for class 8 Mathematic s check out main page of Physics Wallah.