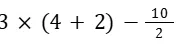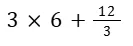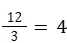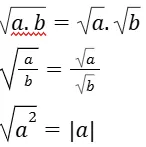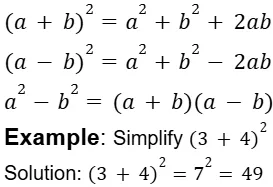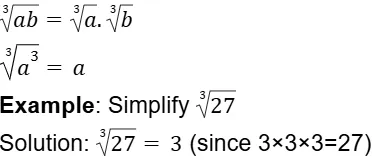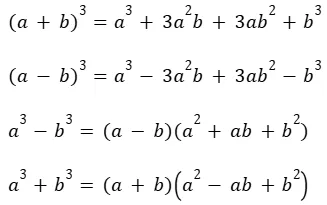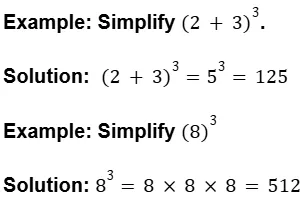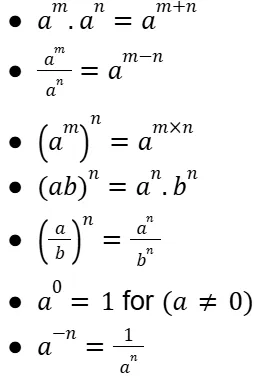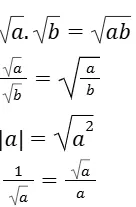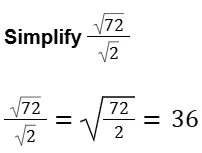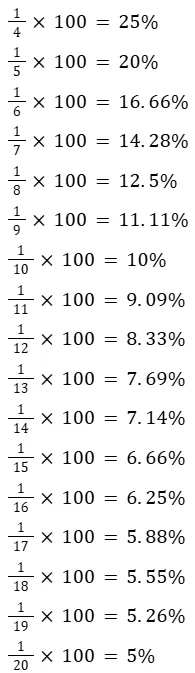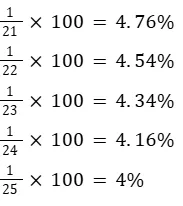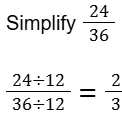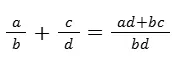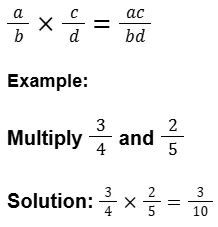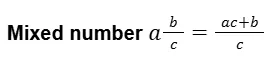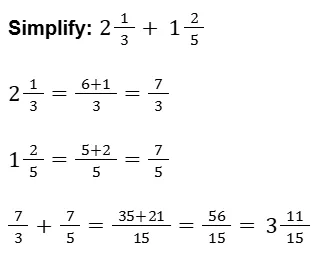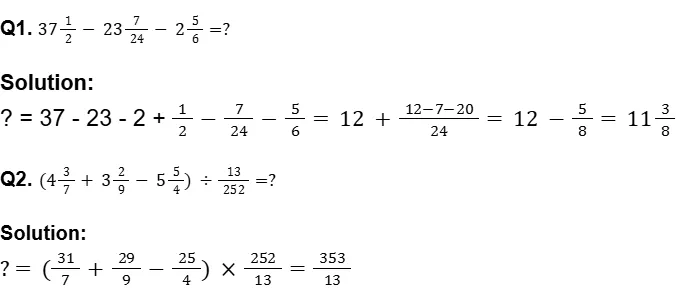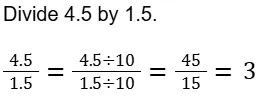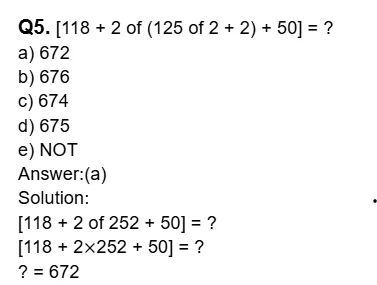They usually involve basic arithmetic operations such as addition, subtraction, multiplication, division, and sometimes powers and roots.
Simplification Questions for IBPS RRB PO and Clerk
Simplification Questions FAQs
Q1. What is Simplification in Quantitative Aptitude?
Ans. Simplification in Quantitative Aptitude involves reducing an expression or equation to its simplest form. This process makes it easier to work with and understand. Simplification can involve combining like terms, reducing fractions, and performing arithmetic operations to make the expression as concise as possible.
Q2. What is the formula of simplification?
Ans. Simplification in math is a process to make math problems simpler. It involves steps like combining terms or reducing fractions. The way you simplify depends on what type of math you're dealing with, like algebra or basic arithmetic. Just follow the order of operations (BODMAS/BIDMAS) for arithmetic – it helps you decide which math steps to do first. If you have a specific math problem, let me know for more help!
Q3. How do I multiply decimals?
Ans. To multiply decimals: Ignore the decimal points and multiply the numbers as whole numbers. Count the total number of decimal places in both numbers. Place the decimal point in the product so that it has the same number of decimal places.
Q4. What is the process for dividing decimals?
Ans. To divide decimals: Move the decimal point in the divisor to the right until it is a whole number. Move the decimal point in the dividend the same number of places to the right. Divide as with whole numbers, and place the decimal point in the quotient accordingly.
Q5. What are some common mistakes to avoid when simplifying expressions?
Ans. Not aligning decimal points properly in addition and subtraction. Forgetting to apply the distributive property when necessary. Not reducing fractions to their simplest form. Incorrectly handling negative signs. Failing to recognize and combine like terms.
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App