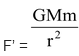NEWTON’s LAWS OF GRAVITATION
Gravitation of Class 9
The magnitudes and the direction of the gravitational force between two particles are given by the universal law of gravitation, which was formulated by Newton. This law is known as Universal law of gravitation.
UNIVERSAL LAW OF GRAVITATION:
Newton's law of gravitation states that every body in this universe attracts every other body with a force, which is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres. The direction of the force is along the line joining the particles.
Mathematical derivation :
The direction of force is along the line joining the centers of two objects.
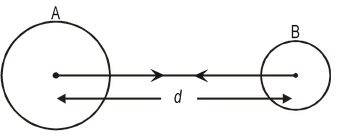
Let two objects A and B of masses M and m lie at a distance d from each other as shown in figure. Let the force of attraction between two objects be F. According to the universal law of gravitation, the force between two objects is directly proportional to the product of their masses. That is,
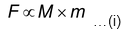 …(i)
…(i)
And the force between two objects is inversely proportional to the square of the distance between them, that is,
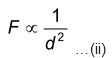 …(ii)
…(ii)
Combining equation (i) and (ii)
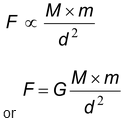
where G is the constant of proportionality and is called as universal gravitation constant.
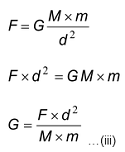
The SI unit of G can be obtained by substituting the unit of force, distance and mass in equation (iii).
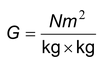
Some importance facts of Universal Law Of Gravitation
The universal law of gravitation successfully explained several phenomena which were believed to be unconnected:
- the force that binds us to the earth;
- the motion of the moon around the earth;
- the motion of planets around the Sun; and
- the tides due to the moon and the Sun.
UNIVERSAL GRAVITATIONAL CONSTANT:
Introduction of Universal constant G: Force of gravitation between two bodies of mass m1 and m2 kept with distance r between their centersis given by the formula :
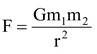
where constant of proportionality G is called universal gravitational constant (U.G.C.).
Definition of Universal constant G :
We know the relation
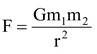
If we put m1 = m 2 = 1, r = 1, then F = G Hence, universal gravitational constant may be defined as the force of attraction between two bodies of unit mass each, when kept with their centers a unit distance apart.
(iii) Units of G:
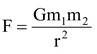
We have,
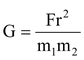
Put the usual notation of all the terms In S.I. unit
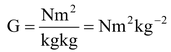
Similarly put the usual notation of all the terms In C.G.S. unit
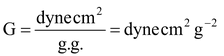
Values of G :
In S.I. G = 6.67 × 10 -11 Nm 2 kg 2
In C.G.S. G = 6.67 × 10 -8 dyne cm 2 g -2
GRAVITATIONAL FORCE BETWEEN LIGHT OBJECTS AND HEAVY OBJECTS:
The formula applied for calculating gravitational force between light objects and heavy objects is the same, i.e.,
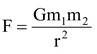 . Let us take three cases:
. Let us take three cases:
1. When two bodies of mass 1 kg each are 1 metre apart.
i.e., m 1 = m 2 = 1kg, r = 1 m
Taking
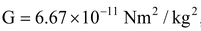 we obtain gravitational force of attraction,
we obtain gravitational force of attraction,
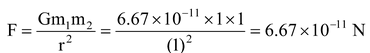
This is extremely small. Hence, we conclude that though every pair of two objects exerts gravitational pull on each other, yet they cannot move towards each other because this gravitational pull is too weak.
2. When a body of mass 1 kg is held on the surface of Earth.
Here, m 1 = 1kg
m 2 = mass of Earth = 6 x 10 24 kg
r = distance of body from centre of Earth
= radius of Earth = 6400 km = 6.4 x 10 3 km = 6.4 x 10 6 m
Gravitational force of attraction between the body and Earth,
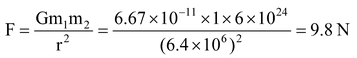
It means that the Earth exerts a gravitational force of 9.8 N on a body of mass 1 kg. This force is much larger as compared to the force when both the bodies are lighter. That is why when a body is dropped from a height, it falls to the Earth.
3. When both the bodies are heavy.
Let us calculate gravitational force of attraction between Earth and the Moon.
Mass of Earth, m 1 = 6 x 10 24 kg
Mass of Moon, m 2 = 7.4 x 10 22 kg
Distance between Earth and Moon, r = 3.84 x 10 5 km = 3.84 x 10 8 m
Gravitational constant, G = 6.67 x 10 -11 Nm 2 /kg 2
The gravitational force between Earth and Moon,
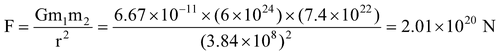
This is really large. It is this large gravitational force exerted by Earth on Moon, which makes the Moon revolve around the Earth.
NEWTON’S THRID LAW OF MOTION AND GRAVITATION:
According to Newton’s third law of motion, for every action, there is an equal and opposite reaction. In other words, we can say that if an object exerts a force on another object, then second object exerts an equal and opposite force on the first object. Since the force of gravitation is also an interaction, therefore, where the earth exerts a force on the object towards it, the object exerts an equal and opposite force towards itself. The question now arises is that if the earth exerts a force and the object is attracted towards it and the object falls towards earth with an acceleration of 9.8 ms –2 , why do not earth gets attracted towards body (why earth does not rise to meet the body?) try to reply it.
According to Newton’s Second Law ,
F = m a or a=Fm
Since the mass of earth is very very large in comparison to a small object and hence acceleration produced in the earth is very very small and cannot be detected with even the most accurate instrument available to us.
From Newton’s second law of motion, we know that :
Force = Mass × Acceleration
So, Acceleration = Force /Mass
or a = F/M
It is clear from this formula that the acceleration produced in a body is inversely proportional to the mass of the body. Now, the mass of a stone is very small, due to which the gravitational force produces a large acceleration in it. Due to large acceleration of stone, we can seen the stone falling towards the earth. The mass of earth it, however, very-very large. Due to the very large mass of the earth, the same gravitational force produces very-very small acceleration in the earth. Actually, the acceleration produced in the earth is so small that it cannot be observed. And hence we do not see the earth rising up towards the stone.
Question Two persons having mass 100kg each, are standing such that the centre of gravity are 1m apart. Calculate the force of gravitation and also calculate the force of gravity on each.
Solution: Given : m1 = m2 = 100kg.
r = 1m. , G = 6.67 × 10 -11 N. m 2 /kg 2
Force of gravitation
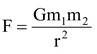
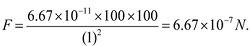
Force of gravity,
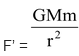 Here r = R, radius of the earth
Here r = R, radius of the earth
and m 1 = M = mass of earth, m 2 = m = mass of object
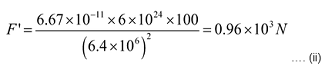
F’ is much greater than F so the persons will not move towards each other but each of them moves towards the earth.
GRAVITATIONAL FORCE BETWEEN DIFFERENT OBJECTS:
Gravitational Force Between Sun and Earth :
Let mass of earth is m 1 = 6 × 10 24 kg
Mass of the sun is m 2 = 7.4 × 10 30 kg
Distance between the sun and the earth, r = 1.5 × 10 11 m
Gravitation force between the sun and the earth,
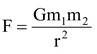
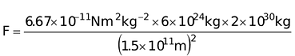
F = 3.6 × 10 22 N
The gravitational force between the sun and the earth is very large (i.e. 3.6 × 10 22 N). This force keeps the earth bound to the sun.
Gravitational Force Between Moon and Earth :
Mass of the earth, m 1 = 6 × 10 24 kg
Mass of the moon, m 2 = 7.4 × 10 22 kg
Distance between the earth and the moon, r = 3.8 × 10 8 m
Gravitational force between the earth and the moon,
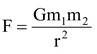
F =
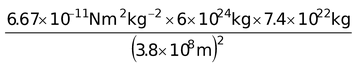
F = 2.05 × 10 20 N
This large gravitational force keeps the moon to move around the earth. This large gravitational force is also responsible fort the ocean tides.
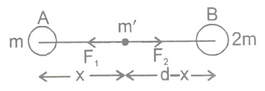
Question 2. Two bodies A and B having mass 4m and 8m respectively are kept at a distance d apart. Where should a small particle be placed so that the net gravitational force on it due to the bodies A and B is zero?
Solution: it is clear that the particle must be placed on the line AB, suppose it is at a distance x from A.
Let its mass is m’.
The force on m’ due to A,
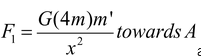 and that due to B is -
and that due to B is -
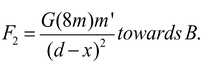
The net force will be zero if F1 = F2
Thus,
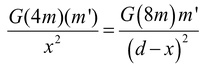
of (d - x) 2 = 2x 2
d - x = ± √2 x
d = ( 1 ± √2) x
x =

As x cannot be negative
So
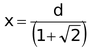
PROPERTIES OF GRAVITATIONAL FORCE.
- It is always attractive in nature while electric and magnetic force can be attractive or repulsive.
- It is independent of the medium between the particles while electric and magnetic force depend on the nature of the medium between the particles.
- It holds good over a wide range of distances. It is found true for interplanetary to inter atomic distances.
- It is a central force i.e. acts along the line joining the centres of two interacting bodies.
-
It is a two-body interaction i.e. gravitational force between two particles is independent of the presence or absence of other particles; so the principle of superposition is valid i.e. force on a particle due to number of particles is the resultant of forces due to individual particles i.e.
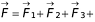 ........
While nuclear force is many body interaction
........
While nuclear force is many body interaction
- It is the weakest force in nature : As Fnuclear> F electromagnetic > F gravitational .
- (The ratio of gravitational force to electrostatic force between two electrons is of the order of 10 -43 .
- It is a conservative force i.e. work done by it is path independent or work done in moving a particle round a closed path under the action of gravitational force is zero.
- It is an action reaction pair i.e. the force with which one body (say earth) attracts the second body (say moon) is equal to the force with which moon attracts the earth. This is in accordance with Newton's third law of motion.
FORCE OF GRAVITATION OF THE EARTH (GRAVITY):
Gravitation and gravity :
Attraction between two bodies having mass of same order, is called gravitation and the force is called gravitational force. Forces involved are very small and the attracting bodies do not move towards each other.
Attraction between a planet (earth) or its satellite and a body, having masses of widely different order is called gravity and the force is called force of gravity. Forces involved are large and body moves towards the planet.
Thus, gravity becomes a special case of gravitation in which small bodies move towards huge planets. Then force of gravity