Equilibrium
Laws Of Motion of Class 11
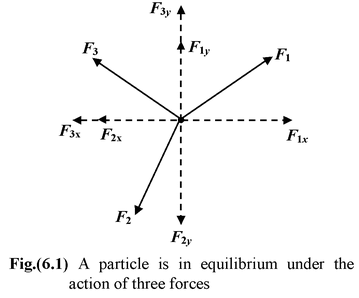
A system is said to be in equilibrium if it does not tend to undergo any further change of its own. Any further change must be produced by external means (e.g. force).
A body is said to be in translational equilibrium if the sum of all the forces acting on the body is zero.
Do follow NCERT Solutions for class 11 Physics prepared by expert faculty of Physics Wallah.
|
Σ
orΣF x = F 1x + F 2x + F 3x = 0(6.2a) andΣF y = F 1y + F 2y + F3y = 0(6.2b)
If the particle is at rest, it is in static equilibrium. whereas if it is moving at a constant velocity, it is in dynamic equilibrium. In either case Σ
|
|
|
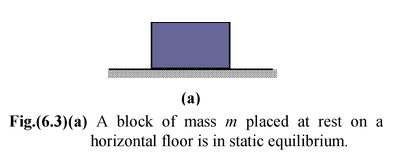
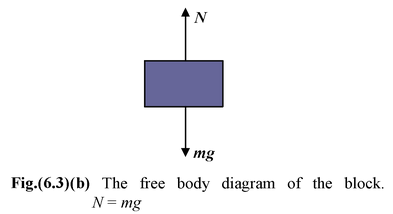
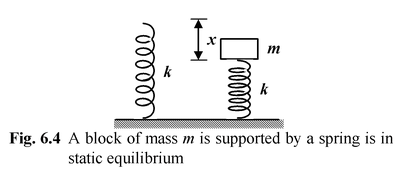
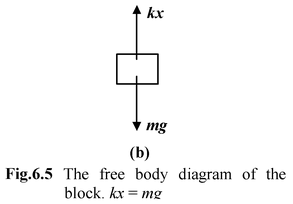
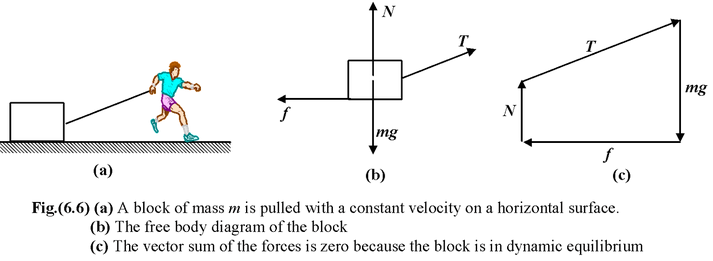
The simplest kind of equilibrium situation is one where two forces act on a body. When you stand motionless. you experience the downward gravitational pull of the earth, your weight W. The weight is balanced by an upward force exerted on you by the floor. This force is perpendicular to the floor and it is called a Normal Force. Some other example of static equilibrium are shown in the Fig. (6.3) to Fig. (6.6). |
|
|
|
|
|
|
|
|
|
|
Problem solving Strategy
1. Make a simple sketch showing the body under consideration.
2. Identify the forces acting on the body, Draw arrows on your sketch to show the direction of
each force acting on the body, in other words, make the free body diagram.
3. Choose a coordinate system and resolve the forces into components that are parallel to the
coordinate axes.
4. Write the equations for equilibrium along each axis of the co−ordinate system.
5. Solve the equations for the required unknown(s).
Example: 6.1
|
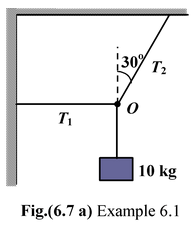
A block of mass 10 kg is suspended with two strings, as shown in the Fig(6.7 a). Find the tension in each string.
(g = 10 m/s 2 ) |
|
Solution
The free body diagram of the joint O is drawn as shown in the Fig. (6.7 b)
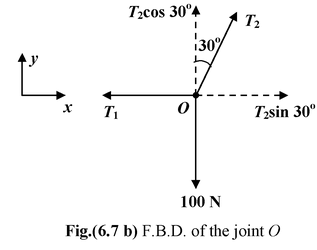
Applying equations for equilibrium.
ΣFx = 0T2sin 30° − T1 = 0..(i)
ΣFy = 0T2cos 30° − 100 = 0..(ii)
Thus,T2 =
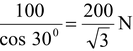
Substituting the value of T2 in equation (i), we get
T1 = T2 sin 30° = 100/√3N
Example : 6.2
|
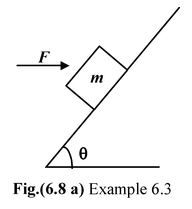
Find the magnitude of the horizontal force F required to keep the block of mass m stationary on the smooth inclined plane as shown in the figure. |
|
Solution
The forces acting on the block are shown in the free body diagram.
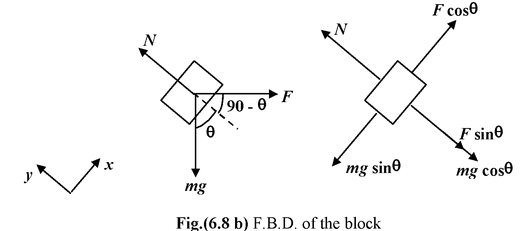
ΣFx = 0
Fcos θ − mg sin θ = 0
or F =
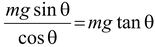
Related Topics