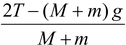Newton's Laws
Laws Of Motion of Class 11
Newton’s First Law
When there is no net force on an object
−an object at rest remains at rest, and
−an object in motion continues to move with a velocity
that is constant in magnitude and direction.
Newton’s Second Law
We know from the first law, what happens when there is no unbalanced force on an object: its velocity remains constant. Now let us see What happens when there is an unbalanced force on an object ? The Newton’s second Law gives the answer to this question, that is, the net force acting on a body will produce an acceleration.
When there is a constant unbalanced force on an object, the object moves with a constant acceleration. Furthermore, if the force varies, the acceleration varies in direct proportion with larger forces producing larger accelerations. Twice the force produces twice the acceleration for the same body.
The magnitude of the acceleration produced depends on the quantity of matter being acted upon. The quantity of matter is referred to as the inertial mass.
Newton’s second law states the relation between the net force and the inertial mass.
ΣF = ma (6.3)
Note that the direction of acceleration is in the direction of the net force.
In terms of components
ΣFx = maxΣFy = mayΣFz = maz(6.4)
IMPORTANT
∙The direction of motion of a particle does not in general coincide with the direction of ∙The acceleration must be measured with respect to an inertial reference frame. |
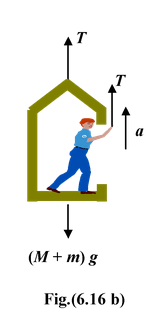
Newton’s Third Law
If the object exerts a force F on a second, then the second object exerts an equal but oppositely force − F on the first.
Example: 6.3
A horse refuses to pull a cart. The horse reasons, “according to Newton’s third law, whatever force I exert on the cart, the cart will exert an equal and opposite force on me so the resultant force will be zero and I will have no chance of accelerating the cart.” What is wrong with this reasoning ?
Solution
|
|
Fig.(6.10)Horse pulling a cart. The cart will accelerate to the right if the force T exerted on it by the horse is greater than the frictional force f exerted on the cart by the ground. The force T′is equal and opposite to T, but because it is exerted on the horse it has no effect on the motion of the cart. |
Figure is a sketch of a horse pulling the cart. Since we are interested in the motion of the cart, we have circled it and indicated the forces acting on it. The force exerted by the horse is labelled T. Other forces on the cart are its weight W, the vertical support force of ground N, and the horizontal force exerted by the ground labeled f (for friction). The vertical forces W and N balance each other. The horizontal forces are T to the right and f to the left. The cart will accelerate if T is greater than f. T′ is the reaction force exerted on the horse, not the cart. It has no effect on the motion of the cart. It does effect the motion of the horse. If the horse is to accelerate to the right, there must be a force F (to the right) exerted by the ground on the horse’s feet that is greater than T′ . This example illustrates the importance of a simple diagram (free body diagram) in solving mechanics problems. Had the horse drawn a simple diagram, he would have seen that he need only push back hard against the ground so that the ground would push him forward.
|
Example: 6.4 Two blocks of mass 2 kg and 3 kg are placed side by side on a smooth surface as shown in the figure. A horizontal force of 10 N is applied on the 3 kg block. |
|
(a)Find the acceleration of each block.
(b)Find the normal reaction between two blocks.
Solution
The free body diagram of each block is drawn as shown in the Fig. (6.11 b) & (6.11 c).
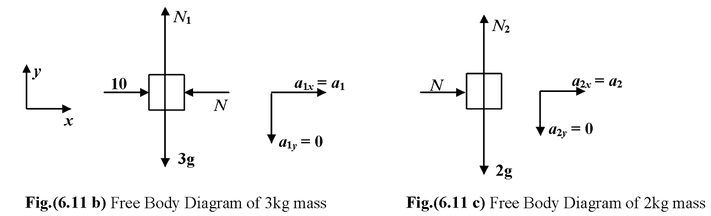
Since the blocks cannot move normal to the surface, therefore. a1y = 0 and a2y = 0. This is called the constraint relation.
Using ΣFx = max for each block, we get
For 3 kg block10 − N = 3a1…(i)
For 2 kg blockN = 2a2…(ii)
(a)Since the blocks are moving together, therefore, a1 = a2 = a
On adding equation (i) and (ii), we get
10 = (3 + 2) a ora = 2m/s2
|
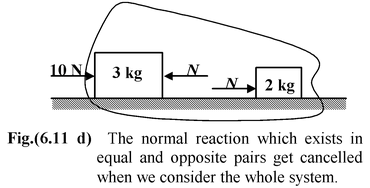
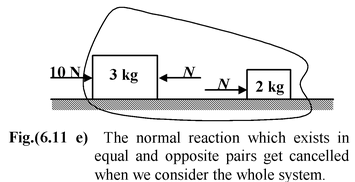
(b)Substituting the value of a in equation (ii), we get N = 2(2) = 4 newton Note that one can easily find the acceleration of the blocks by considering both blocks together as shown in the Fig.(6.11 d) |
|
In this situation, applying Newton’s Second law along the x−axis, we get
ΣFx = max
or10 = (3 + 2) a⇒a = 2 m/s2
Here we have not considered the normal reaction between the blocks − being an internal force it can not accelerate the system (according to Newton’s Third Law).
|
Moreover, the normal reaction exists in equal and opposite pairs, which get cancelled when we consider the whole system. To find out the normal reaction, one can imagine the situation like this : when a force of 10 N acts on the system of blocks each block accelerates with 2 m/s2. |
|
In order to accelerate the 3 kg block with 2 m/s2 we require a force of 6 N but a force of 10 N has been applied, so the remaining force of 10 − 6 = 4 N is transferred to the 2 kg block. Hence, the normal reaction between the two blocks is 4 N.
|
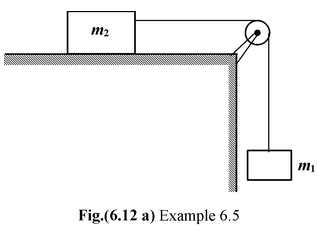
Example : 6.5 A block of mass m2 is placed at rest on a smooth horizontal surface. It is connected to an inextensible string which passes over a smooth pulley and a block of mass m1 is suspended from the other end. (a)Find the acceleration of each block. (b)Find the tension in the string. |
|
Solution
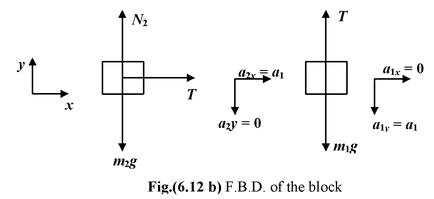
The free body diagram of each block is shown in the Fig. (6.12 b).
Note
- Block m2 can not move vertically; a2y = 0
- No horizontal force acts on block m1; a1x =0
- Since block m1 cannot move downward without making the block m2 to move rightward, and also the vertical distance moved by m1 is equal to the horizontal distance moved by m2,
Therefore, a2 = a1 =
(a)Applying Newton’s Second Law on
Block m1m1g − T = m1a..(i)
Block m2T = m2a.. (ii)
On adding (i) and (ii)
m1g = (m1 + m2) a
ora = 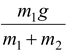
(b)Substituting the value of ‘a’ in equation (ii) we get
T = 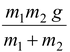
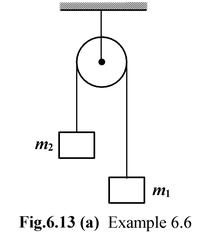
Example: 6.6
|
Two blocks of mass m1 and m2 are attached at the ends of an inextensible string, which passes over a smooth (a)the acceleration of each block (b)the tension in the string. |
|
Solution
The free body diagram of each block is shown in the figure.
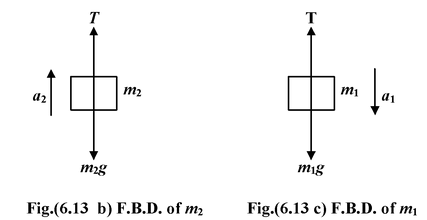
Note
- The block m1 is assumed to be moving downward and the block m2 is assumed to be moving upward. It is merely an assumption and it does not imply the real direction of motion. If the values of a1 and a2 come out to be positive then only the assumed directions are correct; otherwise the bodies move in the opposite directions.
- Since the pulley is smooth and massless, therefore, the tension on each side of the pulley is same.
Applying Newton’s second Law on
Block m1m1g − T = m1a1..(i)
Block m2−m2g + T = m2a2..(ii)
Number of unknowns : T, a1 and a2(three)
Number of equations : only two
Obviously, we require one more equation to solve the problem. Note that the whenever one finds the number of equations less than the number of unknowns, one must think about the constraint relation. In the previous problems we have obtained the constraint relation by experience and judgement. Now we are going to explain the mathematical procedure for this.
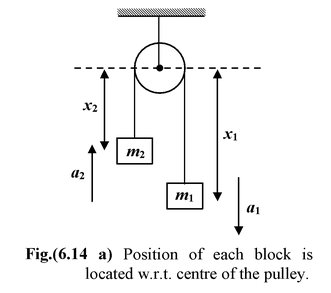
How to determine Constraint Relation ?
|
1.Assume the direction of acceleration of each block, e.g. a1 (downward) and a2 (upward) in this case. 2.Locate the position of each block from a fixed point (depending on convenience), e.g. centre of the pulley in this case. 3.Identify the constraint and write down the equation of constraint in terms of the distance assumed. |
|
For example, in the chosen problem, the length of string remains constant is the constraint or restriction.
Thus,x1 + x2 = constant
Differentiating both the sides w.r.t. time, we get
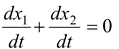
Each term on the left side represents velocity of the block.
Since we have to find a relation between accelerations, therefore, we differentiate it once again w.r.t. time.
Thus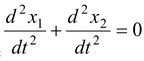
Since the block m1 is assumed to be moving downward (x1 is increasing with time)
∴ 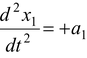 , a1 > 0
, a1 > 0
and block m2 is assumed to be moving upward (x2 is decreasing with time)
∴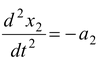 ,a2 > 0
,a2 > 0
Thus a1 − a2 = 0
ora1 = a2 = a
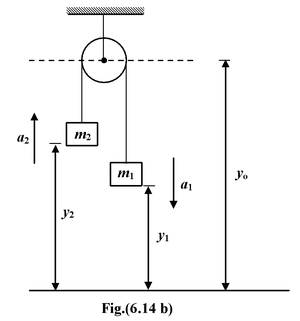
Alternatively, one can also assume the distance of each block from the ground as shown in the figure.
One can easily see that an expression for length of the string can not be written unless we locate the centre of the pulley w.r.t. ground.
|
If y0 be the distance of the ground from the centre of the pulley then the length of string is (y0 −y1) + (y0 − y2) = constant 2y0 − y1 − y2 = constant Differentiating twice w.r.t. time, we get
0 −
Now, Thus a1 − a2 = 0 a1 = a2 = a |
|
Substituting a1 = a2 = a in equations (i) and (ii) and after solving them, we get
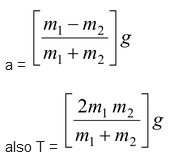
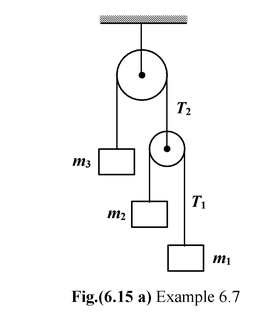
Example 6.7
|
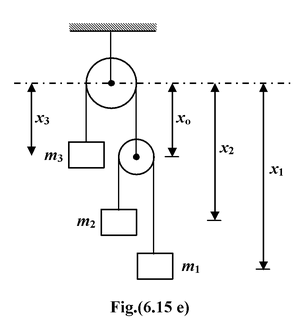
A system of three masses m1, m2 and m3 are shown in the figure. The pulleys are smooth and massless; the strings are massless and inextensible. (a)Find the tensions in the strings (b)Find the acceleration of each mass. |
|
Solution
All the blocks are assumed to be moving downward and the free body diagram of each block is shown in the figure
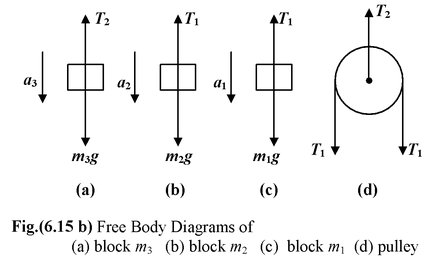
Applying Newton’s Second Law on
Block m1m1g − T1 = m1a1..(i)
Block m2m2g − T1 = m2a2..(ii)
Block m3m3g − T2 = m3a3..(iii)
PulleyT2 = 2T1..(iv)
Number of unknowns : a1, a2, a3, T1 and T2 (Five)
Number of equations : Four
|
The constraint relation among accelerations can be obtained as follows For upper string x3 + x0 = c1 For lower string: (x2 − x0) + (x1 − x0) = c2 x2 + x1 − 2x0 = c2 Eliminating x0 from the above two equations, we get x1 + x2 + 2x3 = 2c1 + c2 = constant Differentiating twice with respect to time. we get |
|
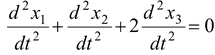
ora1 + a2 + 2a3 = 0…(v)
After solving equations (i) to (v), we get

Example 6.8
|
A 60 kg painter stands on a 15 kg platform. A rope attached to the platform and passing over an overhead pulley allows the painter to raise himself and the platform. (a)To get started, he pulls the rope down with force of 400 N. Find the acceleration of the platform as well as that of the painter. (b)What force must he exert on the rope so as to attain an upward speed of 1 m/s in 1 s. (c)What force should he apply now to maintain the constant speed of 1 m/s. |
|
|
|
Solution The free body diagram of the painter and the platform can be drawn as shown in the figure. Note that the tension in the string is equal to the force by which he pulls the rope. (a)Applying Newton’s Second Law 2T − (M +m)g =(M + m)a
ora = Here M = 60 kg; m = 15 kg; T = 400 N g = 10 m/s a = 2(400) - (60 + 15) (10)/60+15 = 0.67 m/s2 |
|
|
(b)To attain a speed of 1 m/s in one second, the acceleration a must be 1 m/s2.
Thus, the applied force is
F = 1/2(M + m)(g + a) = 1/2 (60 +15) (10+1) = 412.5 N
(c)When the painter and the platform moves (upward) together with a constant speed, it is in a state of dynamic equilibrium.
Thus,2F − (M + m) g = 0
or F = (M + m)g/2 = (60+15)(10)/2 = 375N