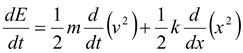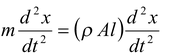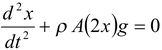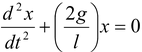Energy Conservation in Simple Harmonic Motion
Simple Harmonic Motion of Class 11
In simple harmonic motion, there's a continuous interchange of kinetic energy (KE) and potential energy (PE). At maximum displacement from the equilibrium point, potential energy is a maximum whereas kinetic energy is zero
In a spring-mass system, the instantaneous potential energy and kinetic energy are expressed as
U =
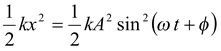 (13.19)
(13.19)
and K =
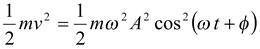 (13.20)
(13.20)
Since ω 2 = k/m , therefore,
K =
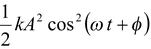
The total mechanical energy is given by
E = K + U
orE =
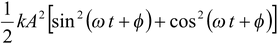
orE =
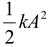 = constant
= constant
|
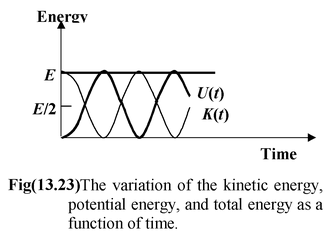
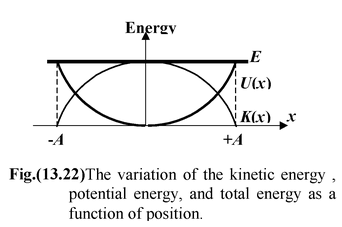
Thus, the total energy of SHM is constant and proportional to the square of the amplitude. The variation of K and U as function of x is shown in figure(13.22). When x = ±A, the kinetic energy is zero and the total energy is equal to the maximum potential energy.
E = Umax =
|
|
There are extreme points or turning points of the SHM.
At x = 0, U = 0 and the energy is purely kinetic,
i.e.E = K
max
=
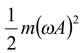
|
The variation of K and U as function of t is shown in figure. Note that the frequency of vibration of the kinetic and potential energy is twice that of the frequency of oscillation. The instantaneous total mechanical energy of the spring-mass system may be written as
E =
Differentiating it w.r.t. time, we get
|
|
or 0 =
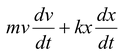
Sincev = dx/dt and
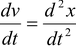 , therefore,
, therefore,
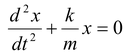
This is the differential equation of SHM.
Example: 13.14
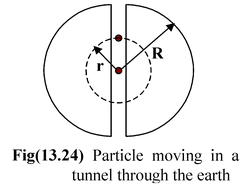
Suppose a tunnel could be dug through the earth from one side to the other along a diameter, as shown in figure(13.24). Show that the motion of the particle is simple harmonic and determine its time period.
|
Solution The gravitational force on the particle at a distance r from the centre of the earth arises entirely from that portion of matter of the earth in shells internal to the position of the particle. The external shells exert no force on the particle. The value of gravity at a distance r is given by g = go r/R |
|
wherego = GM/R 2 is the gravity on the surface of earth.
The net force on the particle is
F = -mg = -mgor/R
Using Newton’s Law,
F =
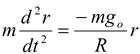
or
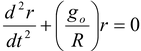
This is the differential equation of SHM.
The period of oscillation is
T = 2π √R/g o
Taking R = 6400 km = 6.4 × 106 m and go = 9.81 m/s2, we get
T = 84.2 min.
Example: 13.15
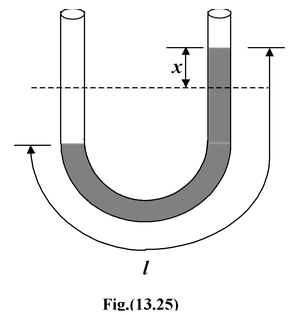
An ideal liquid of density ρ occupies length l of an U – tube of uniform cross-section as shown in the figure(13.25). When the liquid surface is displaced through x the liquid column executes SHM. Find the period of oscillation.
Solution
When the liquid column is displaced through x on the right side, the weight of the unbalanced liquid provides the restoring force.
|
F = -[ρA(2x)]g where A is the area of cross-section Applying Newton’s second law
F =
∴(ρAl)
or
Time period is T = 2π √l/2g |
|
Also Check

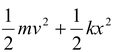 = constant
= constant