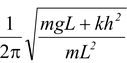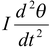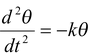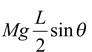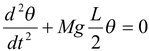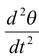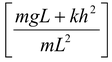Pendulums
Share
Pendulums
Simple Harmonic Motion of Class 11
Simple Pendulum
|
Ideally, a simple pendulum consists of a point mass suspended at the end of a massless string as shown in the fig.(13.16). At the equilibrium position, net torque about the point ‘O’ is zero, at θ = 0. When the pendulum is displaced through an angle θ, the restoring torque about the point O is given by τo = −mglsinθ For small angles sin θ ≈ θ, therefore, τo = −mgl sin θ |
|
Using Newton’s Second Law,
τo = Ioα =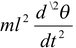 
Thus,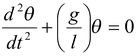
Comparing the above equation with the standard differential equation (13.10), we get
ω2 = g/l
∴T = 
(13.16)
|
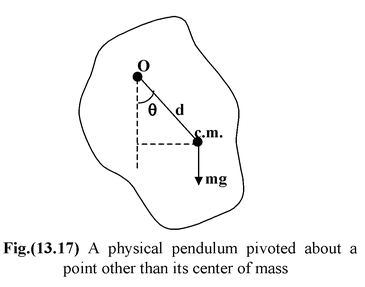
Physical Pendulum In figure (13.17), an extended body is pivoted freely about an axis that does not pass through its center of mass. Such an arrangement forms a physical pendulum that executes simple harmonic motion for small angular displacements. If d is the distance from the pivot to the center of mass, the restoring torque is –mgd sin θ. Using Newton’s Second law, τ = Iα, we get - mgd sin θ = |
|
Where I is the moment of inertia about the given axis. If we use the small-angle approximation, sin θ ≈ θ, then
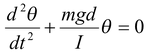
Thus,ω =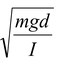 
and T = 2π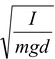 
(13.17)
If the location of the center of mass and d are known, then a measurement of the period allows us to determine the moment of inertia of the body.
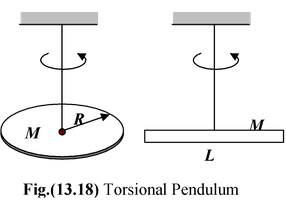
Torsional Pendulum
Consider a body, such as a disc or a rod, suspended at the end of a wire, as shown in the fig.(13.18). When the end of the wire is twisted by an angle θ, the restoring torque is given by τ = -kθ where k is called the torsional constant. Using Newton’s law I or |
|
Thus, the angular frequency and the time period of oscillation are given by
ω = √k/I
andT = 2π √I/k (13.18)
Example: 13.11
|
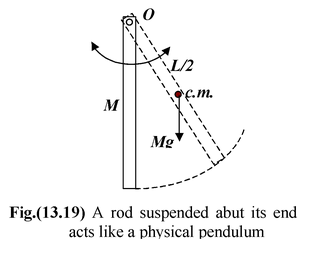
A rod of mass M and length L is pivoted about its end O as shown in the figure(13.19). Find the period of SHM. Find the period of SHM. SolutionRestoring torque is τo = - Using Newton’s Second Law and the small angle approximation, we get Io Using parallel-axes theorem |
|
Io = Ic + 
∴
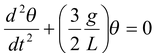
Thus,T = 
Example: 13.12
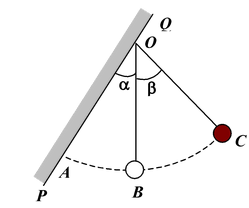
A ball is suspended by a thread of length L at the point O on the wall PQ which is inclined to the vertical by an angle α. The thread with the ball is now displaced through a small angle β away from the vertical and also from the wall. If the ball is released, find the period of oscillation of the pendulum when
(a) β < α(b) β > α.
Assume the collision on the wall to be perfectly elastic.
Solution
The motion of simple pendulum is angular SHM; so its equation of motion will be
θ = θo sin ωt with ω = √(g/L)
|
(a)When β < α, i.e., when angular amplitude β is lesser than α, the pendulum will oscillate with its natural frequency, so that T1 = 2π/ω = 2π √L/g (i) (b)When β > α, time taken by pendulum to move from B to C and back to B, |
|
t1 =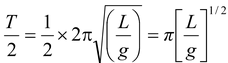 
(ii)
Now as in case of simple harmonic motion
θ = θo sin ωt
So time taken by the pendulum to move from equilibrium position B to A,
i.e., for θ = α when θo = β, will be given by
α = β sin ωt, i.e., t =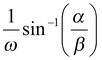 
So time taken by pendulum to move from B to A and back to B,
t2 = 2t =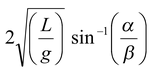 
(since ω = √(g/L) )
So time period of motion
T2 = t1 + t2 =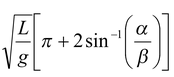 
Example: 13.13
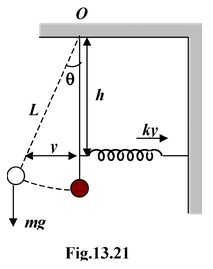
A simple pendulum of length L and mass m has as spring of force constant k connected to it at a distance h below its point of suspension. Find the frequency of vibrations of the system for small values of amplitude.
Solution
As shown in figure, if the pendulum is given a small angular displacement θ, the spring will also stretch by y ( = h tan θ). So there restoring torque about O will be due to both force of gravity and elastic force of the spring.
i.e. τ = -[mg(L sin θ) + k(h tan θ)h]
|
Now for small θ, tan θ = sin θ = θ soτ = -(mgL + kh2)θ i.e. restoring torque is linear, so motion is angular SHM. Now as τ = Iα = mL2 (as I = mL2) so with ω2 = |
|
This is the standard equation of angular SHM with frequency f = (ω/2π); so here
f = 
