

Workdone by variable force is a concept in physics that involves calculating the amount of energy transferred when an object is subjected to a force that changes in magnitude or direction as the object moves. To calculate the work done by a variable force, you typically need to use calculus, specifically integration, because the force is not constant over the entire distance the object moves.
The formula for calculating work done by a variable force F(x) over a given distance is given by: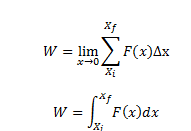 Where:
- W is the work done (measured in joules, J).
- F(x) is the variable force as a function of position \(x\).
- dx represents an infinitesimally small displacement along the path of motion.
- xf and xi are the initial and final positions, respectively, of the object.
Here are the basic steps to calculate the work done by a variable force:
Where:
- W is the work done (measured in joules, J).
- F(x) is the variable force as a function of position \(x\).
- dx represents an infinitesimally small displacement along the path of motion.
- xf and xi are the initial and final positions, respectively, of the object.
Here are the basic steps to calculate the work done by a variable force:
- Determine the expression for the force as a function of position, \(F(x)\). This could be given in the problem statement or derived from a physical model.
- Identify the initial and final positions of the object, \(x_1\) and \(x_2\).
- Set up the integral from \(x_1\) to \(x_2\) with \(F(x)\) as the integrand and \(dx\) as the differential displacement.
- Evaluate the definite integral to find the work done.
Also Check - Thermodynamics formula
It's important to note that the direction of the force and the direction of motion should be taken into account when calculating work done. If the force and the displacement are not in the same direction, you may need to use vector dot product notation or break the force into components parallel and perpendicular to the displacement. Also, remember that work done by a force can be positive, negative, or zero, depending on whether the force helps, opposes, or has no effect on the motion of the object. In some cases, when the force varies continuously and is expressed as a mathematical function, you can use integration to calculate the work done precisely. However, if the force varies discretely (e.g., in steps), you can approximate the work done by breaking the motion into smaller segments and calculating the work done in each segment, then summing them up.Also Check - Work, Energy & Power Formula
Examples Workdone By Variable Force
Here are 10 theoretical examples of calculating work done by variable forces, each with a brief explanation:- Spring Force:
- Gravitational Force:
- Frictional Force:
Also Check - Unit, Dimension & Vector Formula
- Electric Force:
- Magnetic Force:
- Tension in a Rope:
- Gas Expansion:
- Variable Wind Resistance:
- Stretching a Rubber Band:
- Fluid Resistance:
Workdone By a Variable Force Formula FAQs
What is the definition of work in physics?
In physics, work is the measure of energy transfer that occurs when a force acts on an object and causes it to move a certain distance in the direction of the force.
How is work related to force and displacement?
Work (W) is calculated by multiplying the force (F) applied to an object by the displacement (d) it undergoes in the direction of the force, using the formula: W = F *d
What are the units of work?
The SI unit of work is the joule (J), which is equivalent to one newton-meter (1 N·m). In other systems, work may be expressed in units such as foot-pounds or ergs.
What does negative work mean in physics?
Negative work occurs when the force applied to an object opposes its motion or direction of displacement. It signifies that energy is being taken away from the object's kinetic energy.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App











