
Additive Inverse: Every number has an opposite that perfectly cancels it out. This concept, called the additive inverse, is fundamental to understanding mathematical relationships and solving equations.
Whether dealing with real numbers, complex numbers, or algebraic expressions, the additive inverse helps balance and simplify calculations. In this blog, we will explore the applications of the additive inverse in real and complex numbers with solved examples.
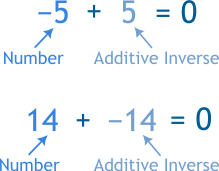
Read More: Median of a Triangle
What is Additive Inverse?
The additive inverse of a number is the value that, when added to the original number, gives a sum of zero. Simply put, it’s the opposite of the number. If the number is positive, its additive inverse is negative, and if the number is negative, its additive inverse is positive. This works because a number and its opposite cancel each other out. For example, the additive inverse of 6 is -6, because 6 + (-6) equals 0. Similarly, the additive inverse of -9 is 9, because -9 + 9 also equals 0. Even zero has an additive inverse, which is itself, because 0 + 0 equals 0. Imagine you have 5 candies and you give all 5 away. Now, you have nothing left. This is like adding 5 and -5 to get 0. Similarly, if you have a debt of $10 (represented as -10) and repay $10, your balance becomes zero. This concept of canceling out a number with its opposite is what defines the additive inverse.Properties of Additive Inverse
The properties of the additive inverse, derived from negating the original number, are outlined below.- Double Negation: −(−a) = a
- Square Property: (−a) 2 = a 2
- Distributive Over Addition: −(a+b) = (−a)+(−b)
- Distributive Over Subtraction: −(a−b) = (−a)+b
- Subtraction of Negative: a−(−b) = a+b
- Multiplication with a Negative Factor: (−a)⋅b = a⋅(−b) =−(a⋅b)
- Product of Two Negatives: (−a)⋅(−b) = a⋅b
Additive Inverse of Real Numbers
The additive inverse of a real number is the value that, when added to the original number, results in a sum of zero. Essentially, the additive inverse is the opposite of the given number. The concept applies to all real numbers, which include natural numbers, whole numbers, integers, fractions, decimals, rational numbers, and irrational numbers. Let’s understand this in detail with clear examples for each type of number.Additive Inverse of Natural Numbers
Natural numbers are counting numbers starting from 1, and they are always positive. The additive inverse of a natural number is its negative counterpart. For example, the additive inverse of 5 is −5, because 5 + (−5)=0.Additive Inverse of Whole Numbers
Whole numbers include all natural numbers and zero. The additive inverse of a positive whole number is its negative. For instance, the additive inverse of 7 is −7. However, zero is an exception because its additive inverse is itself: 0 + 0 = 0.Additive Inverse of Integers
Integers include positive numbers, negative numbers, and zero. For positive integers, the additive inverse is the negative version. For example, the additive inverse of 3 is −3. For negative integers, the additive inverse is the positive version, as multiplying by −1 reverses the sign. For example, the additive inverse of −6 is 6, because −6 + 6 = 0. For zero, its additive inverse remains zero.Additive Inverse of Fractions
Fractions are positive unless stated otherwise. The additive inverse of a fraction is the negative version. If a fraction is a/b, its additive inverse is −a/b For instance, the additive inverse of 2/3 is −2/3 because 2/3 + (−2/3) = 0.Additive Inverse of Rational Numbers
Rational numbers can be either positive or negative. The additive inverse is found by multiplying the number by −1. For a positive rational number p/q, its additive inverse is −p/q. For a negative rational number −p/q, its additive inverse is p/q. For example, the additive inverse of 5/4 is −5/4, and the additive inverse of −3/7 is 3/7.Additive Inverse of Decimals
A decimal consists of a whole part and a fractional part. The additive inverse involves changing the sign of the entire number. For example, the additive inverse of 2.35 is −2.35, and the additive inverse of −0.2 is 0.2.Additive Inverse of Irrational Numbers
Irrational numbers include non-terminating, non-repeating decimals and roots of non-perfect squares or cubes. The additive inverse is obtained by multiplying the number by −1. For example, the additive inverse of √2 is -√2, because √2 +(−√2)=0 . Similarly, the additive inverse of , the additive inverse is −2 + , becauseAdditive Inverse of Complex Numbers
A complex number is written in the form a + ib , where a and b are real numbers, and i represents the imaginary unit (√-1). The additive inverse of a complex number is another complex number that, when added to the original, results in zero (0 + i0). In other words, for a complex number a + ib , its additive inverse is c + id , such that:(a+ib) + (c+id) = 0 + i0
How It Works:
To find the additive inverse of a + ib , we simply take the negative of both the real and imaginary parts. This means the additive inverse is -a - ib . For example:- The additive inverse of -3 + 2i is 3 - 2i .
- The additive inverse of a + 3i is -a - 3i .
Additive Inverse of Algebraic Expressions
The additive inverse concept applies to algebraic expressions , which are combinations of variables and constants. To find the additive inverse of an algebraic expression, multiply every term in the expression by -1. This flips the sign of each term (positive becomes negative, and negative becomes positive). When the original expression and its additive inverse are added, the result is always zero.How It Works:
For any algebraic expression P(x), the additive inverse is −P(x) If P(x) = ax n + bx n−1 + ⋯+c, its additive inverse is: −P(x) =−ax n − bx n−1 −⋯−cAdditive Inverse and Multiplicative Inverse
The following table outlines the differences between additive and multiplicative inverses, incorporating insights from the provided references and practical examples.|
Difference Between Additive Inverse and Multiplicative Inverse |
||
| Aspect | Additive Inverse | Multiplicative Inverse |
| Definition | The additive inverse of a number a is the number −a. | The multiplicative inverse of a non-zero number a is 1/a. |
| Notation | Represented as −a | Represented as 1/a or |
| Objective | Balances the number to zero when added. | Balances the number to one when multiplied. |
| Applicability | Applicable to all real numbers, including zero. | Applicable only to non-zero numbers (zero has no multiplicative inverse) |
| Outcome | Adding a number to its additive inverse gives zero: a+(−a)=0 | Multiplying a number by its multiplicative inverse gives one: a× (1/a)= 1. |
| Similarities | Both involve operations that "cancel out" the original number in their respective contexts. | Both are used to simplify equations and mathematical expressions. |
| Applications | Additive inverses are used in mathematics, physics, and economics to solve equations, simplify expressions, and balance values. | Multiplicative inverses are used in algebra to isolate variables (e.g., 2x = 8 ⇒ x= 4), and in calculus to simplify functions like 1/f(x). |
Additive Inverse Solved Examples
Example 1 : Find the additive inverse of 2/3x−4/5. Solution: The additive inverse of each term in the expression is obtained by multiplying by −1: Additive inverse = − ( 2/3 x − 4/5 ) = − 2/3 x + 4/5 Verification: (2/3x−4/5) + (−2/3x+4/5) = 2/3x − 2/3x−4/5 + 4/5 = 0Example 2: Find the additive inverse of 2+3i−5
Solution: The additive inverse of each part is obtained by flipping the sign: Additive inverse= −1⋅(2+ √3i−√5) = −2− √3i + √5 Verification: (2+√3i−√5) + (−2−√3i+√5) = 2−2+√3i − √3i − √5 +√5 = 0Example 5: Find the additive inverse of 4x 2 y−7xy 2 +5z−8
Solution: Multiply each term in the expression by −1. Additive inverse = −(4xy 2 − 7xy 2 + + 5z − 8) = 4x 2 y + 7xy 2 - 5z + 8 Verification: (4x 2 y − 7xy 2 + 5z − 8) + (-4x 2 y + 7xy 2 - 5z + 8)| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| Composite Numbers | Differentiation |
| Perimeter of Rectangle | Surface Area of Cylinder |
Additive Inverse FAQs
How does the additive inverse differ from the multiplicative inverse?
The additive inverse cancels a number to make the sum zero, while the multiplicative inverse cancels a number to make the product one.
Can the additive inverse simplify logarithmic equations?
Yes, in log(a)+log(−a)=, the additive inverse negates the log arguments
How does the additive inverse work in modular arithmetic?
Imodular arithmetic, the adn ditive inverse of a is the number that, when added to a, gives a remainder of zero.
What is the additive inverse in three-dimensional space?
In 3D space, the additive inverse of a point (x,y,z)is (−x,−y,−z)
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App








