
Area of a Parallelogram
Have you ever looked at a slanted shape and wondered how to measure the space inside it? How do architects calculate floor areas for unusual room shapes, or how do designers create perfectly measured patterns for tiles and artwork? The answer lies in understanding the area of parallelogram.
Unlike rectangles, parallelograms may seem tricky due to their slanted sides, but with the right approach, calculating their area is simple and incredibly useful.
From construction and farming to graphic design and physics, mastering the area of parallelogram helps solve real-world problems In this blog, we will learn to calculate the area of a parallelogram using three different formulas .
Read More - Arithmetic Progression
What is a Parallelogram?
A parallelogram is a four-sided polygon, also known as a quadrilateral, characterized by having:
- Two pairs of parallel sides (opposite sides are parallel).
- Opposite sides of equal length .
- Opposite angles of equal measure .
- Diagonals that intersect each other .
Examples of Parallelograms
- Rectangle : Opposite sides are equal, and all angles are 90°.
- Rhombus : All sides are equal, but angles may vary.
- Square : All sides are equal, and all angles are 90°.
- Classic Parallelogram : Opposite sides and opposite angles are equal, but none of the angles have to be 90°.
Understanding the Area of a Parallelogram
The area of parallelogram is the measure of the region enclosed within its boundaries. Unlike the perimeter, which measures the total distance around the shape, the area represents the amount of space the parallelogram covers. The area is expressed in square units (e.g., square centimeters, square meters, square inches).
Key Terms for Calculating Area
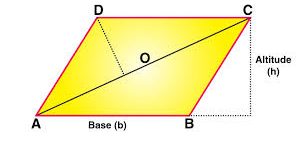
- Base (b) : Any side of the parallelogram chosen as the base.
- Height (h) : The perpendicular distance between the base and the opposite side.
Why Does the Area Formula for a Parallelogram Work?
To understand why the area formula for a parallelogram works, think of a parallelogram as a slanted rectangle.
Imagine taking a triangular piece from one side of the parallelogram and moving it to the other side. When you do this, the parallelogram turns into a rectangle. The base and height of the shape stay the same during this process.
The area remains the same since the base and height don’t change. That’s why the formula for the area of parallelogram is the same as for a rectangle:
Area= Base × Height (A= b × h)
This simple idea shows that even though a parallelogram looks slanted, its area can still be measured like a rectangle.
How to Find the area of Parallelogram?
The area of a parallelogram, which is expressed in square units (such as cm2, m2, in2, etc.), is the total number of unit squares that may fit within it. In two dimensions, it is the area that a parallelogram encloses or encompasses. A parallelogram is a two-dimensional, four-sided shape having two opposing sets of parallel sides.
In our everyday lives, we see different geometric shapes besides rectangles and squares. Because a parallelogram and a rectangle share few characteristics, the area of a parallelogram is comparable to that of a rectangle.
Area of a Parallelogram Formulas
Here are the different formulas for calculating the area of parallelogram
Basic Formula: Using Base and Height
The most straightforward method for calculating the area of a parallelogram is by using the base and height.
Parallelogram area formula:
Area= Base × Height (A= b × h)
- b : Length of the base
- h : Perpendicular height
Example If the base of a parallelogram is 7 cm and the height is 12 cm, the area is:
7 cm ×12 cm = 84 cm 2
Read More - Quadrilateral: Definition, Types, Properties, Examples
Using Side Lengths and Angles
If the height is unknown, but you know the lengths of two adjacent sides and the angle between them, you can use trigonometry to find the area.
Formula:
A=a × b× sin(θ)A
- a and b : Lengths of adjacent sides
- θ : Angle between the sides
Example: If two adjacent sides are 8 cm and 6 cm and the angle between them is 45° , the area is:
8 × 6 ×sin(45°)= 48 × 0.707 = 33.94 cm 2
Using Diagonals and Angle Between Them
If you know the lengths of the diagonals and the angle between them, you can calculate the area using the following formula:
Formula:
A=1/2× d 1 ×d 2 ×sin(y)A
- d₁ and d₂ : Lengths of the diagonals
- y : Angle between the diagonals
Example Calculation: If the diagonals are 10 cm and 14 cm , and the angle between them is 60° , the area is:
1/2× 10 × 14 × sin(60°) = 70× 0.866= 60.62 cm 2
Perimeter of a Parallelogram Formula
The perimeter of a parallelogram is the total distance around its outer edges. Calculating its perimeter is straightforward because a parallelogram has two pairs of opposite sides that are equal in length.
Understanding the Sides of a Parallelogram
In a parallelogram:
- The two longer sides are equal in length.
- The two shorter sides are also equal in length.
Let’s label the sides as:
- Side AB = Side CD = b (the longer sides)
- Side BC = Side AD = a (the shorter sides)
Perimeter Formula
The formula to calculate the perimeter of a parallelogram is:
Perimeter=2×(Length+Width)
This formula works because you are adding the lengths of the two pairs of equal sides.
Example 1: Classic Parallelogram
Suppose you have a parallelogram with:
- Length (b) = 12 cm
- Width (a) = 7 cm
To find the perimeter:
Perimeter=2×(12 cm+7 cm)=2×19 cm=38 cm
Example 2: Parallelogram Shaped Tile
Imagine a tile shaped like a parallelogram where:
- Each long side is 15 inches
- Each short side is 9 inches
The perimeter is:
Perimeter=2×(15 inches+9 inches)=2×24 inches=48 inches
Example 3: A Field in the Shape of a Parallelogram
Suppose a farmer’s field is a parallelogram with:
- Long sides measuring 100 meters
- Short sides measuring 60 meters
To calculate the perimeter of the field:
Perimeter=2×(100 m+60 m)=2×160 m=320 m
Area of a Parallelogram Applications
Knowing how to calculate the area of a parallelogram is useful in many everyday situations. Here are some simple examples:
Building and Construction
Floor Planning : Helps measure floor areas for rooms with unusual shapes.
Material Estimation : Helps figure out how much material you need for things like roofs, tiles, or wall panels.
Farming and Land Measurement
Field Size : Useful for measuring the size of farmland or fields.
Irrigation Planning : Helps plan watering systems by knowing the exact size of the land.
Art and Design
Pattern Making : Useful for creating accurate patterns in quilting, tiling, and mosaics.
Graphic Design : Helps design geometric shapes and patterns in art projects.
These simple examples show why knowing how to calculate the area of a parallelogram is important in everyday life!
Tips for Calculating the Area of a Parallelogram
Mastering the area of a parallelogram is easy with these essential tips:
- Always use the perpendicular height , not the slanted side length. The height must form a right angle with the base.
- If the height isn’t given, use the formula with side lengths and the angle between them: Area=a×b×sin(θ)
- Make sure all measurements are in the same units before calculating. Express the final area in square units (e.g., cm², m²).
- Applying these formulas to practical examples such as calculating the area of a floor plan, a plot of land, or a piece of fabric reinforces your understanding and improves your problem-solving skills.
Solved Area of a Parallelogram Examples
A room has the shape of a parallelogram with a base of 12 meters and a height of 8 meters . What is the floor area of the room?
Solution: The formula for the area of a parallelogram is:
Area=Base×Height
- Base ( b ) = 12 m
- Height ( h ) = 8 m
Area=12 m×8 m=96 m 2
Answer: The floor area of the room is 96 square meters .
Example 2: A fabric piece for a quilt is shaped like a parallelogram with two adjacent sides of 8 cm and 6 cm , and the angle between them is 45° . What is the area of the fabric piece?
Solution: The formula for the area of a parallelogram using side lengths and an angle is:
Area=a×b×sin(θ)
Given:
- Side length ( a ) = 8 cm
- Side length ( b ) = 6 cm
- Angle ( θ ) = 45°
Area = 8 cm × 6 cm ×sin(45∘)
Answer: The area of the fabric piece is 33.94 square centimeters .
Example 3: A farmer's field is shaped like a parallelogram with diagonals of 10 meters and 14 meters , and the angle between them is 60° . Calculate the area of the field.
Solution: The formula for the area of a parallelogram using diagonals and the angle between them is:
Area=1/2×d1×d2×sin(y)
Given:
- Diagonal ( d₁ ) = 10 m
- Diagonal ( d₂ ) = 14 m
- Angle ( y ) = 60°
Area=1/2×10 m×14 m×sin(60∘)
= 1/2×140×0.866= 60.62 m 2
Answer: The area of the field is 60.62 square meters .
Understanding the area of a parallelogram and its various calculation methods is a valuable skill in both academics and real-world applications.
By mastering these formulas and concepts, you’ll be better equipped to tackle problems in mathematics, construction, design, and beyond.
Whether you’re a student learning geometry or a professional applying these concepts in your field, calculating the area of a parallelogram is a fundamental tool that proves useful time and time again. Join Online Tuition for Kids Now!!
| Related Articles | |
| Ordinal Numbers | Area of Rectangle |
| Natural Numbers | Even Numbers |
| Angles | Multiplication Sums |
Area of a Parallelogram FAQs
How does the area of a parallelogram change if the shape becomes more slanted?
Can two parallelograms with different shapes have the same area?
Can a parallelogram area be negative?
Can I use any side of a parallelogram as the base?
What real-world objects resemble parallelograms?









