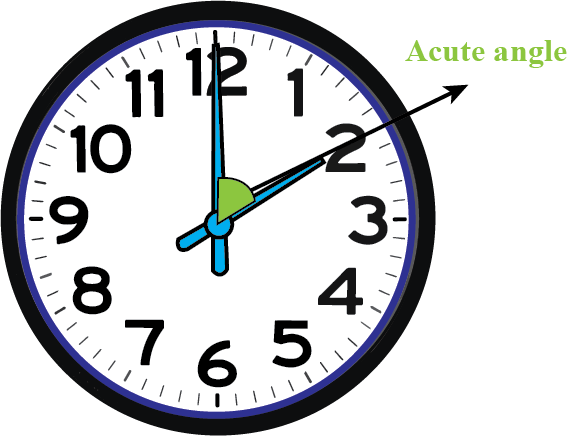
Acute Angle
Acute Angle meaning: An Acute angle measures greater than 0 ∘ but less than 90 ∘, forming a sharp, narrow opening when two rays meet at a common point. These angles appear in countless shapes and structures around us, from the blades of scissors to the hands of a clock. Curious to learn more about what is acute angle and how it appears in daily life? Let’s explore its acute angle definition and see acute angle examples in the real world.
What Are Acute Angles?
To create solid foundations in geometry, it is critical to grasp the acute angle definition. When compared to a straight angle or obtuse angle, an acute angle is sharper since it is less than 90 degrees. When we define an acute angle, we simply mean any angle that is less than a right angle
Acute Angle Shape
An acute angle resembles a sharp wedge or a narrow slice of pie. It is less than 90° and forms a pointed, narrow shape. For instance, imagine the tip of an arrow—the angle at the point is an acute angle.
Picture a slightly open book; the small angle formed between the two covers is acute.
The vertex is where the two arms of the angle meet, much like the tip of the arrow or the narrow end of the pie slice.
The arms are the two lines that extend from the vertex, similar to the two edges of the pie slice or the covers of the book. These arms spread apart but remain within a sharp angle, always less than 90°.
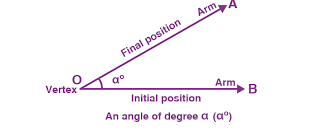
Where Are Acute Angles Found?
Students always ask what is a acute angle, and the basic answer is that it is a small angle seen in a number of forms and figures. There are acute angles all around us! When you look at a clock telling 2:00, the hands make a tiny angle; it is an acute angle. A pizza slice also has one acute angle-a pointy one. When you look at the roof of your house or the crazy angles of a star, all acute angles. You will now start seeing acute angles everywhere!
Why Are Acute Angles Important in Maths
Acute angles have great application value! They are used in drawing, building houses, making signs, and even in art. Suppose you want to make shapes like triangles or stars; you will need an acute angle to make the shapes. Understanding the meaning of acute angles and applying the acute angle formula will help you to learn more. So learning about acute angles is both fun and useful!
Acute Angle Degree (0° to 90°)
An acute angle degree is defined as any angle that measures greater than 0° and less than 90°. The acute angle formula can be expressed as:
0° < Measure of Acute Angle < 90°
In simpler terms, any angle within this range is considered acute. For example, angles such as 25°, 47°, 63°, 78°, and 89° are all acute angles.
This guideline makes it easy to identify acute angles by simply checking their degree measurement. The definition of acute angle is simple: it is any angle that is greater than 0° but less than 90°.
Check Out - Hyperbola: Definition, Equation, Properties, and Examples
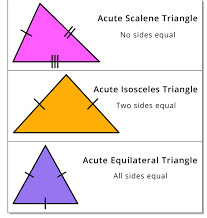
Acute Angled Triangle
The acute angle triangle is a typical example, where each of the triangle's three internal angles is acute and less than 90 degrees. This type of triangle is always sharp and narrow at each corner. A special case of an acute triangle is an equilateral triangle , where all three angles measure exactly 60°.
Acute triangles can be further classified into three categories based on their sides:
Acute Scalene Triangle : All angles are acute, and all sides are of different lengths.
Acute Isosceles Triangle : All angles are acute, with two sides of equal length.
Equilateral Triangle : All three sides and angles are equal, with each angle measuring 60°.
Acute Angled Triangles Formula
The triangle inequality theorem describes an important formula for acute triangles. This theorem helps us identify if a triangle is acute using its sides. Apply the acute angle formula from the triangle inequality theorem to check.
If a triangle has sides labeled as a, b, and c (where c is the longest side), the triangle is acute if:
a 2 + b 2 > c 2
This condition ensures that the sum of the squares of the two shorter sides is greater than the square of the longest side. Similar conditions apply for all permutations of the sides: c 2 + b 2 > a 2
a 2 + c 2 > b 2
By verifying these inequalities, you can determine if a triangle is acute, regardless of how its sides are labeled. These relationships ensure that all angles in the triangle are less than 90°.
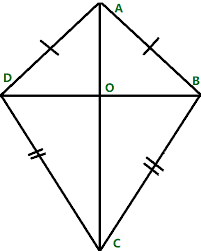
Acute Angle in Quadrilateral
In a quadrilateral, which is any four-sided shape, an acute angle is an angle that measures less than 90°. These sharp, narrow angles differ from the right angles typically found in squares or rectangles.
For instance, in a kite-shaped quadrilateral, two of its corners often form acute angles.
Acute Angle in Polygon
In regular polygons, where all sides and angles are equal, acute angles are usually absent.
For example, a regular pentagon or hexagon has interior angles greater than 90°, making them obtuse instead of acute.
However, in irregular polygons, such as a five-sided figure with unequal sides and angles, acute angles can appear where corners are sharper and measure less than 90°.
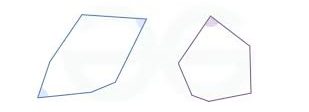
Acute Angle in Irregular Shapes
Irregular shapes often include acute angles because their sides and angles vary. For example, in a star-shaped polygon, the pointed tips are acute angles. Similarly, a randomly drawn five-sided figure might have a mix of acute and obtuse angles, with acute angles appearing wherever the corners are sharper.
Acute Angle in Composite Shapes
Composite shapes, which are formed by combining two or more simple shapes, can also include acute angles. For example:
- Joining a rectangle with a triangle creates a composite shape where the triangle’s sharp corners are acute angles.
- In a house-shaped figure (a rectangle topped with a triangle), the roof's sharp points form acute angles.
In composite shapes, any corner measuring less than 90° is classified as an acute angle
Check Out - Ratio: Meaning, Formulas, How to Solve, Types, Examples
Acute Angle vs Obtuse Angle vs Right Angle
Angles are categorized based on their measurements, and understanding the differences between acute, obtuse, and right angles is essential for geometry and everyday applications. Here's a simple explanation of each:
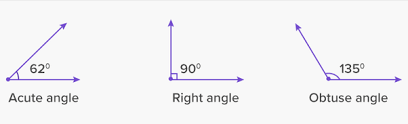
Acute Angle:
- An acute angle measures less than 90° .
- It is sharp and narrow, appearing in shapes like acute-angled triangles where all three angles are acute.
- Example: An angle measuring 60° is an acute angle.
Right Angle:
- A right angle measures exactly 90° .
- It forms a perfect L shape and is present in right-angled triangles, where one angle is always a right angle.
- Example: An angle measuring 90° is a right angle.
Obtuse Angle:
- An obtuse angle measures greater than 90° but less than 180° .
- It is wide and open, commonly found in obtuse-angled triangles where one angle is obtuse.
- Example: An angle measuring 120° is an obtuse angle.
Let's Play Hide & Seek at Home!
The Acute Angles are going to hide, and we have to seek. It is your turn to look for acute angles indoors. Just observe all the places in your house where two lines or edges create a very small pointy angle. Do you see the one between a pair of scissors? What about the fine corner at the end of a slice of pizza? Just try to shape a "V" with your fingers - see that acute angle? Draw a triangle and find all the tiny angles within. Count how many acute angles you'll find, and ask your parents to help too. Let's make it fun as a family activity!
Acute Angle Examples
Triangles with all of their angles less than 90 degrees are known as acute angle triangles. Learn what an acute angle is, which is just an angle that is less than a straight angle, before you can understand this. When we define an acute angle, we mean one that is always less than 90 degrees. Because of this, these triangles have a sharp, narrow form. Here are some examples given below:
Example 1: Angle A measures x degrees. Determine if A is acute for the following values: x = 15°, x = 65°, x = 90°°, and x = 135
Solution:
When x = 15°
15°<90°
Yes,∠A is an acute angle.
When x = 65°
65° < 90°
Yes, ∠A is an acute angle.
When x = 90°
90° = 90°
Since an acute angle must be strictly less than 90°, ∠A is not acute.
When x = 135°
135° > 90
No, ∠A is not acute.
Example 2: A triangle has sides a = 5, b = 6, and c = 7. Is the triangle acute ?
Solution:
To verify, apply the acute angle formula:
Check a 2 + b 2 > c 2
5 2 + 6 2 = 25 + 36 = 61 > 7 2 or 49 True.
Check b 2 + c 2 > a 2
6 2 + 7 2 = 36 + 49 = 85 > 5 2 or 25
True.
Check c 2 + a 2 > b 2
7 2 + 5 2 = 49 + 25 = 74 > 6 2 or 36
True.
Since all conditions are satisfied, the triangle is acute. Join Online Tuition Class for Kids Now !!
| Related Articles | |
| Area of Rectangle | Isosceles Triangle |
| Composite Numbers | Triangle |
| Perimeter of Rectangle | Surface Area of Cylinder |
Acute Angle FAQs
How many acute angles can a triangle have?
Can an obtuse triangle have an acute angle?
What is the smallest acute angle?
What is an example of an acute angle in sports?